Why Ranked-Choice Voting Might Make Little Difference In Heavily Contested Primaries

One advantage of using primaries to select nominees for President is that when the selection process takes place over time, it is easier for similarly-minded voters to coordinate on nominees. Today is a good illustration, as the departures of Pete Buttigieg and Amy Klobuchar from the race for the Democratic nomination facilitate the coordination of moderate Democrats, presumably to the benefit of Joe Biden. Whatever one's politics, it may seem perverse that the more candidates who cluster around a particular set of issue positions, the greater the advantage for candidates outside the cluster. And it may also seem perverse that candidates sometimes must drop out to best address the ideological interests of their supporters.

Social choice theorists have identified alternative approaches to resolving elections in a single round that in theory avoid imposing a disadvantage on clustered candidates. These mechanisms require voters to rank either all candidates or some of their favorites in preference order. The mechanism that seems to receive the most attention these days is ranked-choice voting. This algorithm, sometimes referred to as instant runoff voting, eliminates candidates one by one based on who has the fewest first-place votes; when a voter's first-place candidate is eliminated, the second-place candidate assumes the top spot.

Ranked-choice voting, however, does not have a desirable property, known as the Condorcet criterion. An algorithm meets this criterion if it guarantees that it will always select a candidate who beats all other candidates in pair-wise comparisons, should such a candidate exist. For example, suppose 45% of voters have the preference ordering (1) Left (2) Center (3) Right, 40% have the preference ordering (1) Right (2) Center (3) Left, and 15% have Center as their first choice. Then, a majority of voters prefer Center to Left, and a majority prefer Center to Right, so a Condorcet method would choose Center. But ranked-choice voting would eliminate Center, ultimately selecting Left instead.

Defenders of ranked-choice voting suggest that this is highly unlikely in practice. For example, an analysis of 138 elections in the Bay Area using ranked-choice voting found that each election of the 138 had a Condorcet winner and that the ranked-choice mechanism in fact selected this winner. This may seem surprising, given the simplicity of the example above in which a Condorcet winner exists but ranked-choice voting does not select it. Another surprising result is that only 7 of the 138 elections chose a candidate trailing in the first round, indicating that ranked-choice voting rarely produces a result different from that of a system that simply chooses the candidate with the most first-place votes.

One possible explanation for these phenomena is that voters ranking their preferred candidates are not doing so in a vacuum, but instead are placing some weight on other voters' preferences. Political scientists have long noted the possibility of bandwagon effects, and it is plausible that a voter might want to vote for the election winner, or at least for a candidate who is the obvious alternative to the winner. Voters might do this even with a voting system in which they rank all their choices. A related possibility is that a voter does not want to "waste" a vote and seeks to act strategically, even though ranked-choice voting and Condorcet methods greatly limit (without eliminating) the possibility of strategic behavior. A voter who deep down prefers Elizabeth Warren, for example, might mistakenly believe that placing her near the top of the ballot will limit the voter's ability to make a choice between Bernie Sanders and Biden. We can think of this as a bandwagon effect too, though the motivation is quite different.

If voters change their heart-of-hearts rankings to favor candidates who are more popular among other voters, adoption of ranked-choice voting might make little difference. Consider, for example, a ranked-choice poll from about a week ago of Democratic primary voters. Given the rankings of voters, Sanders was the Condorcet winner and also would have won a ranked-choice vote, though with only a narrow head-to-head edge over Biden. This is in part because 27% of Sanders voters had Biden as a second choice and 38% of Biden voters had Sanders as a second choice. These results may seem surprising given the conventional wisdom that Sanders and Biden are in separate lanes, but makes perfect sense if there are some voters who will tend to place the candidates who have the best chance of winning at the top of their ranked-choice ballot.

To what extend do bandwagon effects undermine Condorcet methods? As a quick back-of-the-envelope approach, I ran a simple simulation many times (C# source code here). The gist is that I assumed that there are 10 candidates, each of whom has two attribute values randomly distributed from 0 to 1. Each voter also has a preferred value for each attribute and ranks candidates based on the sum of the absolute difference from the voter's preference to each candidate's attribute value. However, half of voters are susceptible to a bandwagon effect, in which they give some benefit to the two candidates who have the highest number of first-place votes overall. I then varied the size of this bandwagon effect.

This simulation allows us to distinguish latent Condorcet winners from apparent Condorcet winners. A latent Condorcet winner is a candidate who beats all other candidates in pair-wise comparisons when there are no bandwagon effects. An apparent Condorcet winner is a candidate who beats all other candidates in pair-wise comparisons when bandwagon effects exist. Arguably, we would like an election method to tend to choose latent Condorcet winners, even though voters' revealed rankings factor in bandwagon effects.

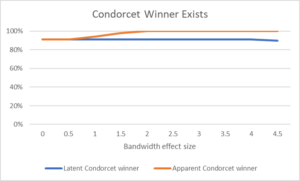
This simulation can help us answer whether bandwagon effects explain why apparent Condorcet winners seem to exist so often and why ranked-choice voting picks these so often. The figure immediately below shows how often the simulation produced latent and apparent Condorcet winners. With no bandwagon effects, Condorcet winners exist around 90% of the time; the other 10% of the time, some form of the Condorcet paradox emerges. But as bandwagon effects increase, the proportion of the time that a Condorcet winner emerges rises to 100%. Unfortunately, these are apparent Condorcet winners, reflecting how the voters vote but not necessarily the assumed latent preferences. This helps explain the result above that a Condorcet winner almost always appears to exist.

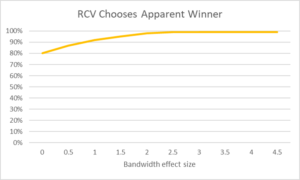
Similarly, the next figure demonstrates that the probability that ranked-choice voting chooses the apparent winner increases with bandwagon effects. Of cases in which an apparent Condorcet winner exists, ranked-choice voting succeeds at identifying that winner only 80% of the time in our simulations without bandwagon effects, but 100% of the time when the bandwagon effects are large. Again, this helps explain the result that ranked-choice voting seems to choose Condorcet winners, despite the absence of theoretical guarantees that it will do so.

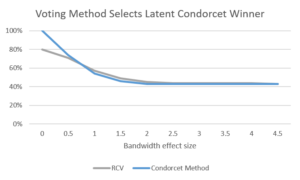
Changing from ranked-choice voting to a Condorcet method will not much improve the voting system's chance of selecting the latent Condorcet winner. The next chart illustrates the probability that a voting method selects the latent Condorcet winner. Condorcet methods are better than ranked-choice voting in the absence of bandwagon effects, but both are equally bad given bandwagon effects.

This suggests that when implementing some form of preference balloting in elections with many candidates, the most important challenge is to persuade voters that they should reveal their true preferences and shouldn't worry about wasting their votes. Perhaps this information might be easier to convey with ranked-choice voting than with more complex Condorcet methods, because the dynamics of ranked-choice voting are more intuitively understood. If so, ranked-choice voting might be preferable to Condorcet methods, despite the latter's stronger theoretical properties. On the other hand, the superficial very strong apparent performance of ranked-choice voting may reveal that it is not easy to convince voters to express their true preferences. If that's so, seemingly more primitive voting systems, such as our own Presidential primary system, could be preferable.

This analysis doesn't tell us much about whether some type of Condorcet method might make a difference in a general election with a very small number of candidates. It seems plausible that adopting such a method might allow for the emergence of a centrist third party in the United States. Ranked-choice voting would be unlikely to make a difference, since the centrist candidate would have the fewest votes. But it seems plausible that a centrist candidate might be able to convince many voters to place her second on the ballot, and a Condorcet method could then choose this candidate as the winner. Precisely for this reason, ranked-choice voting, which makes little difference, may be much more politically feasible than a Condorcet alternative.