How the War on Drugs Fails Black Communities
Despite generally higher usage rates among white Americans, black Americans are three times likelier to be arrested for possession.
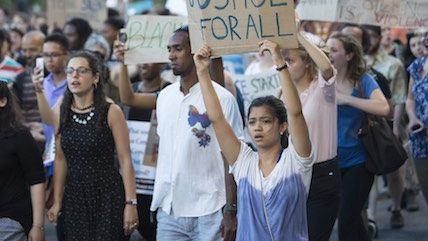
As recent events have demonstrated, more than 50 years after much-delayed civil rights legislation was passed by Congress and signed into law, very different views on the persistence of racism still exist in America. According to the Pew Research Center, 38 percent of whites believe that "our country has made the changes needed to give blacks equal rights with whites," but just 8 percent of blacks agree.
Here's something that all Americans should agree on: Many policies have a disproportionately negative effect on black families—and, by extension, on all of us. The most insidious of them all, however, may be the war on drugs.
Writing for the Cato Institute, John McWhorter noted: "It has become a norm for black children to grow up in single-parent homes, their fathers away in prison for long spells and barely knowing them. In poor and working-class black America, a man and a woman raising their children together is, of all things, an unusual sight." The drug war plays an oversize role in this trend.
Keeping drugs illegal makes selling them more profitable than they would otherwise be. As such, the war on drugs creates incentives for young black men to seek employment in the drug business rather than seek lower-paying legal employment. This incentive structure unfortunately starts a vicious circle of incarceration followed by "a failure to build the job skills for legal employment that serve as a foundation for a productive existence in middle and later life," McWhorter continued.
And for what? By all accounts, the decadeslong war on drugs has failed miserably. Despite our spending over $1 trillion to stop the stoner scourge, overall drug consumption has barely changed, and some drug prices are falling because of technology and increasing supply. Also, drug addiction has gone up while seeking treatment has become riskier.
In addition, incarceration rates for drug offenses have skyrocketed since the 1980s because of mandatory sentencing laws, which rigidly determine who goes to prison and for how long. Nonviolent drug offenders account for about one-fourth of inmates in the United States, up from less than 10 percent in 1980. It destroys families and leaves children to be raised in single-parent households. This is particularly true for low-income black families. Despite generally higher usage rates among white Americans, black Americans are three times likelier to be arrested for possession.
A byproduct of the war on drugs is civil asset forfeiture, which gives police officers the ability to seize private property that they claim is connected to illegal activity without actually charging the property owner with a crime, much less convicting him. The abuses that come with the practice have been widely documented. Studies also show that black and Hispanic Americans are disproportionately targeted. A recent analysis of high-dollar forfeiture cases by Oklahoma Watch found that officers, knowingly or not, use racial profiling when deciding whose vehicles they will search and whose money and assets they will seize.
The Libertarian presidential candidate, Gary Johnson, is talking about legalizing marijuana as a first step to ending the drug war, but neither the Republican (Donald Trump) nor the Democratic (Hillary Clinton) candidate is. The lack of interest in the issue is shocking for Clinton, who belongs to a party that claims to care about low-income Americans and receives an overwhelming majority of the black vote. Yet it would also serve Republicans well to oppose the drug war, because they claim to naturally oppose big-government policies that dictate what individuals can or cannot choose to consume—whether it be soda, salt or sativa.
The drug war isn't the only policy that disproportionately hurts African-American families. Minimum wage laws keep low-income Americans from getting jobs, and Social Security redistributes money from minorities to white Americans. Both are also overlooked as a source of unfairness to the black community.
However, as McWhorter noted, "what will turn black America around for good is the elimination of a policy (the drug war) that prevents too many people from doing their best." When that happens, with the help of time, we will make black lives better and, in turn, make America better.
COPYRIGHT 2016 CREATORS.COM



Show Comments (93)