Parents on Common Core: Stop Using Our Kids As Guinea Pigs

Michael Reilly / Facebook

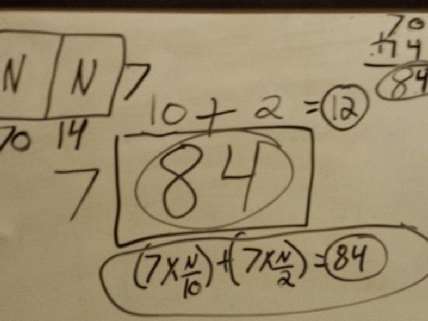
Common Core is still making parents everywhere pull their hair out as they struggle to help their kids solve Byzantine math problems. Silive.com profiled some very frustrated parents who believe their kids are essentially being used as "guinea pigs" by government and corporate interests in service of an unproven teaching methodology:

Ten-year-old Kate Reilly, a fifth-grader at PS 55 in Eltingville, was doing math homework, seated around the kitchen table with her younger sister, Emma, a second-grader at PS 55, and older brother, John, who attends Bernstein Intermediate School, Huguenot.

One of her math problems called for dividing 84 by 7. Looking over her shoulder, watching her jot down pre-alegbriac equations as she successfully solved the problem, her dad, Michael Reilly, just shook his head.

"This is just ridiculous. 84 divided by 7. Why are we making this harder than it has to be? " he wondered.

Frustrated, Reilly posted a photo of the problem to his Facebook page. Within minutes it drew close to 200 comments from equally frustrated, puzzled parents.

Reilly isn't just any parent; he is also president of the Staten Island Community Education Council and frequently hears from other parents who are fed up with Core-aligned methodology and requirements.

Just because a certain way of learning is confusing for parents doesn't make it inherently bad, of course. It's perfectly possible for educators to invent an approach that makes math easier for kids, even if older generations don't get it.

But it's hard to believe that that's what is happening here, since many teachers and students seem just as hopelessly lost as parents. Misaligned tests, improper training for teachers, and Common Core's uncertain political future are all factors adding to the confusion. And even if the standards eventually catch on and have a positive impact on American education—and the evidence there is underwhelming—the kids caught in the transition years will have been undeniably ill-served. It's no wonder that some students resent being forced to serve as conscripted product testers for Core-aligned examinations.

More from Reason on Common Core here.

Comments

[Fist of Etiquette]

IT'S TWELVE! The answer is 12.

[Pro Libertate]

It's hard to believe that this system, which serves to make education more difficult for those teaching outside of formal education (esp. homeschoolers), isn't at least partly intended for that purpose.

[Square]

My sister-in-law works for one of the think-tanks that developed the standards.

As developed (in the private sector) the standards are imminently rational.

Put those standards in the hands of government, and Common Core is what you get.

There's nothing sinister about the particular methods being implemented, but the idea of a "Common Core," i.e. a universal standard governing how every child in the country is to be educated, is fundamentally flawed, whatever its content may be.

And yes, the intent is to solidify federal hegemony over education nationally.

[Pro Libertate]

Yes, it's something relatively benign made horrific by the introduction of politics into something that shouldn't have even a lick of politics in it.

[Fluffy]

This is the entire purpose.

They want to create a situation where talented people and homeschooled people won't outscore public school zombies on standardized tests.

Since there was no way to do that for real math, they decided to make up reams of fake math that they can now put on to standardized tests.

[anon]

From the pic, I can't understand what the kid did to arrive at the answer, but my question is still what's wrong with actually using ... division?

[Stormy Dragon]

84 / 7 = (70 + 14) / 7 = 70 / 7 + 14 / 7 = 10 + 2 = 12

[anon]

Right, but how did she arrive at "70 + 14," guess and check? It defeats the whole point of "learning" division.

85 / 7 would leave the kid unable to answer.

[Zeb]

Old fashioned long division would be easier in that case, for sure (or just memorize multiplication tables). But I can see some sense to learning that process if it is done appropriately by people who really understand why you might want to do it that way (which doesn't seem too likely given the mathematical sophistication of most elementary school teachers).

[Square]

"if it is done appropriately by people who really understand why you might want to do it that way"

Therein lies the rub. Common Core + teachers unions = disaster.

[trshmnster the terrible]

. But I can see some sense to learning that process if it is done appropriately by people who really understand why you might want to do it that way

Yep, it should be taught that (or a similar) way in 5th or 6th grade as a "now that you've mastered division, let me show you a shortcut to do it in your head" trick.

[waffles]

It looks like they're supposed to break it down to the nearest integer * 10. I'm not convinced this is easier than teaching that 7 * 12 = 12 + 12 + 12 + 12 + 12 + 12 + 12.

[anon]

I thought that at first too, but that'd be (80+5)/7 in this case. Must be the nearest integer with a factor higher than the divisor.

[anon]

woops, meant 80+4.

[waffles]

84 / 7 = (80 + 4) / 7 = 77/7 + 3/7 + 4/7 = 11 + 1 = 12

Common Core Rules Suckaz!

[Kaptious Kristen]

That's my question, too. How did she know where to start? Why not start with 80+4? Or 60+24?

Not to mention not everyone's brain reasons the same way. I've said it a jillion times, so-called "education experts" should be looking for ways to efficiently diversify learning models, not make everyone learn the same way.

[Zeb]

"education experts" should be looking for ways to efficiently diversify learning models, not make everyone learn the same way.

That is really the problem with something like common core. These methods and algorithms are probably great for some kids and completely counterproductive for others.

[Square]

That's the sickest thing. The point of the theory was that you should present different methods of problem solving because different children's brains process things differently, and they should be free to use what works best for them.

What the government standards people decided was that all children should be forced to master all conceivable methods.

[Bobarian (dinosaur hunter)]

The SICKEST thing is that only brain damaged fucks that can't handle real subjects get education degrees and become 'education experts'!

[Restoring the Dream]

Absolutely! You have to be exposed to bunches of numbers to get a feel for them. No experience with numbers and you'll never be able to smell a wrong answer. That's the problem with calculator trained people- in real life it's often not needed to know a correct answer, but to spot wrong ones intuitively.

[Stormy Dragon]

7 goes into 8 once, so 84 / 7 = 10 + some value determined through additional calculation.

e.g. the first thing you do in traditional long division.

[trshmnster the terrible]

That's not what's going on here.

It's 7x10=70 (assumes child has multiplication tables memorized to 10)

70 is close to, but less than 84,so it's a good one to start with. (assumes mastery of 2 digit greater than/less than, and ability to get close to the target dividend with the memorized multiplication tables)

84-70=14 (assumes mastery of 2 digit subtraction)

7x2 =14

10+2=12 (assumes child is organized enough to keep track of all multiplication factors they did)

Otoh, for long division, it goes like this:

Is 8 greater than 7? (assumes mastery of 1 digit greater than/less than)

Yes. Is 8 greater than 7x2? (assumes mastery of multiplication table up to 2,and low 2 digit gt/let mastery)

No. Place a 1 in the tens position of the quotient. (assumes the child can remember instructuons)

8-7=1 (assumes mastery of single digit subtraction).

Is 1 greater than 7?

No.drop down the 4 (assumes can follow instructions)

Is 14 gt 7 (low 2 dig comparison)

Yes. Is 14 gt 7x2? (mult table to 2)

No, but it's equal (remember instructions)

Place 2 above the 4

14-14=0 (low 2 dig subtraction)

Are there any digits left (following instructions)

No. Is there any remainder left? No.

Done. More steps, but much less strenuous assumptions for a 3rd grader who may or may not have a subconscious grasp of the previous math materials.

Try doing the common core method with a kid who only has the multiplication table memorized to 2. It's a page and a half of work.

[Rasilio]

70 is the nearest multiple of 10 which is also a multiple of 7.

The basic idea is you never do division and avoid subtraction as much as possible, so you try to rephrase all questions to only multiplication and addition wherever possible. Then you don't waste your time memorizing the multiplication tables for all single digits but rather just the columns that follow easy to memorize patterns (1, 2, 3, 5, and 10) then you break all problems down into combinations using those numbers because the mathematical operations are so simple.

So 85 /7 becomes...

85 = 70 + 15

15 is not a multiple of 7 so find the greatest multiple of 7 below 15

85 = 70 + 14 + 1

85/7 = ((7 * 10)/7) + ((7 * 2)/7) + 1/7

85 = 10 + 2 + 1/7

85 = 12 1/7 or 12 remainder 1 depending on the form you want it in.

[waffles]

Is that how common core does all maths?

98 / 17 = (90 + 8) / 17 = 90 / 17 + 8 / 17 = 98 / 17 (punch into calculator ) = 5.765

It doesn't seem easier. In fact, why are they teaching students to separate like terms instead of combining them?

[Zeb]

It seems to me as if they are teaching them useful heuristics for doing mental arithmetic. But I have no idea how it is actually being taught, so that might not be the actual result.

[Curt]

No... breaking 98 into (90 + 8) doesn't make any sense because 90 isn't evenly divisible by 17. The concept works best when you're dividing by single digits.

98/7 = (70 + 28) /7 = 70/7 + 28/7 = 10+4 =14.

98/6 = (60 + 38) /6 = (60+36+2)/6 = 60/6 + 36/6 + 2/6 = 10+6+(1/3) = 16 and 1/3

[Curt]

In fairness, I don't know exactly how they teach it. I'm too old and I don't have kids. But the approach seems obvious to me. Essentially it's an introduction to algebra without introducing all of those scary letters.

It seems reasonable enough and it generally matches the way that I do math in my head. I understand this is always taught after the "normal" way. But, with substandard teachers and parents that don't get it, I'm not surprised that this is a big FAIL.

[Curt]

another example with bigger numbers:

153/6 = (120+33)/6 = (120+30+3)/6 = 120/6 + 30/6 + 3/6 = 20 + 5 + 0.5 = 25.5

basically you break the numerator into chunks that are easily divisible by the denominator

[Stormy Dragon]

Which coincidentally is the exact same way you do it in traditional long division. All that's changed here is the notation to make the fact the algorithm is an application of the distributive principle more explicit. This is important for the children to understand later on when you want them to get how to solve a problem like dividing a^3 + b^3 + a^2 * b^2 + a * b by a^2 + b

This "outrage" is the equivalent who learned differential equations in Newton's notation flipping out because their kid is using Leibniz's notation.

[Cyto]

It is more than that. They are trying to teach multiple approaches for solving the same equations. My second grader is really struggling with this idea. He knows how to solve the problem one way, and now they are telling him to do a different set of steps (that will engrain a deeper mathematical concept). He can do it the first way he learned in a couple of seconds - so the second and third way they introduce are extremely difficult for him to grasp.

For the parent it is also tough... first you have to understand the instructions as written - often difficult because they are dependent on a lesson that was delivered at school. Then you have to discern the concept they are trying to teach - tough enough for a science major with a doctorate, let alone for the semi-literate vocational school grad. Also with no help in the instructions or any indication other than the actual construct of the questions.

Both my wife and I have graduate level educations and we have run into problems understanding the questions in first grade homework. Not because there is anything difficult about adding 13 + 6, but because there are multiple visualization techniques at play that are not explained in any context available to the parents.

[Curt]

I think you hit on the main problem. The school doesn't teach parents what they're doing, so the parents have no idea how to coach their kid through it. But, the school expects that this will happen.

Also, I think 2nd grade is way too young for this kind of thing. I never truly learned things like the distributive property until high school algebra. I had been doing it without knowing it for years, but never really had it explained. No one taught me, I was just comfortable enough with math to detour from the normal, vanilla approach because it was too slow.

Public school teachers trying to teach this to 2nd graders is like a drunk uncle taking the training wheels of a kid's bike and telling him to ride down a hill, go off a jump, and do a flip.

[trshmnster the terrible]

That's such a shitty way to do division, because

A) it assumes they have the multiplication tables memorized
B) it assumes the divisor will be less than 10
C) it assumes the quotient to be an integer

Try 2048/16 using the same method... It doesn't fucking scale unless you know your hex multiples. Even assuming that the child knows multiples of 16 up to 64, it'll take a page of paper to write down all the shit they need to show their work.

If you aren't convinced, try 16/3 with that approach. How about 17/4.5?

Long division works because you don't have to change your method based on the answer (that you don't know yet). Common Core division is the way I do rough estimating or the most simple math problems in my head. Mainly because I remember the lower half of the multiplication table faster than the upper half.

[robc]

^^THIS^^

This is the exact right answer.

[kinnath]

Me (at bakery counter): I'll take four brownies (98 cents each)

Clerk: reaches for paper and pencil.

Me: that's $4.92

Clerk: dumb look.

Me: That's 4 bucks minus 8 cents equals $4.92.

Clerk: dumb look.

Me: I'm an engineer -- trust me.

[kinnath]

fooking typo 😉

[kinnath]

twice even.

[Muzzle of Bees]

$3.92.

You're a good tipper.

[Curt]

Me (at Dunkin Donuts a few weeks ago): I'll take six individual donuts (99 cents each)

Clerk rings me up for a half dozen ($5.99)

Me: No, I said I'd like six individual donuts

Clerk explains that a half dozen is 6.

Me: I'm aware of that, ring me up for 6 individual donuts

Clerk changes my order and new total is $5.94. Promptly calls the manager over.

I'm pretty sure they are still scratching their heads while staring at cash register and price sign. Haven't been to another DD to see if that's the standard pricing scheme or just that one store.

[anon]

Long division works because you don't have to change your method based on the answer (that you don't know yet).

Yeah, that's essentially the point I was making.

[anon]

To which I'll add, if you already know the answer, there's no point in solving a problem that doesn't exist.

[Stormy Dragon]

The above problem IS long division. It's just being written down differently.

7 / 84:

7 goes into 8 once, so you write down 1 (whic is really 10 because it's in the tens place)

subtract 1 * 7 from 8 to get 1, pull down the 4 to get 14 left (which is really breaking 84 up into 70 + 14)

7 goes into 14 twice, so add 2 to the one from before (which is 10 + 2 = 12)

It's the EXACT same method this girl did. All that change is she had to explicitly write down the application of the distributive property which is only implied the traditional way.

[Curt]

It's not a shitty way to do division, just a shitty way for a public school to teach kids to do division. The kids don't understand math well enough yet to do it effectively. The teachers don't understand the concept well enough to explain it effectively.

In fairness, I think that they always give them simple problems with relatively simple, integer denominators. But, maybe, maybe, if you teach them that they can do things like this, they'll realize they can use other tricks to simplify things.

-- 2048/16... divide num&denom; by 2 = 1024/8... repeat = 512/4... repeat = 256/2... repeat = 128.

-- 16/3 = (15+1)/3 = 15/3 + 1/3 = 5 and 1/3.

-- 17/4.5... double num&denom; = 34/9 = (27+7)/9 = 27/9 + 7/9 = 3 and 7/9

Don't get me wrong... 90% of students (especially young ones) won't think this way or understand these approaches. The problem isn't that the approach is bad... it's that a public school is trying to force it on students who aren't ready/capable.

[kinnath]

And this is bullshit for fifth grade.

[Stormy Dragon]

So the daughter got the right answer and is also appears to be getting preparation for the introduction of algebra later on.

Other than purely knee jerk "when I was your age we only got to eat gravel and we LIKED it that way" bullshit, why exactly am I supposed to be outraged by this?

[Zeb]

I have a similar reaction. The math stuff I have seen from common core does seem to have some decent reasoning behind it. I have no idea if it will work better than the old fashioned way, and I tend to agree that just memorizing multiplication tables for numbers under 12 is probably a good thing. But it's not just new and complicated for its own sake.

The one criticism I would make is that I would like to see some actual evidence that this improves students' later performance in math. I've always "gotten" math, so I have no idea how the mind of someone who doesn't works.

[anon]

Another thing I'd add, is multiplication tables teach more than just multiplication. They teach you how to group information for easy reference and/or memorization.

Spreadsheets, etc.

[Warren]

Um, no I don't think so. Maybe they're a child's first introduction to using a table. But that's not much.

[Agile Cyborg]

My kids have been using common core in rural Ohio for about 3 years now. I totally understand a lot of the static about top-down authoritative imposition of centrally-planned methodologies in education... However, I'm not totally derisive of common core. As one who has done his fair share of programming over the years the way math is being taught even in the early grades kind of reminds me of the simple math philosophy behind beginner software coding.

Sure, it seems overly-complex in light of how simple memorization is to those of us who've been taught far differently but kids growing up with this kind of math are far more likely to grasp computer languages.

[Zeb]

That's an interesting point.

[Fluffy]

The reason you should be outraged by this is because the entire reason - and I mean the ENTIRE reason - it's being done is because if you subject a mixed group of public school and private school / homeschool kids to a standardized test that just supplies division questions and grades the kids on whether they can get the right answer, the private school and homeschool kids score better.

So the public school establishment has invented an entirely new set of questions, where the answer doesn't matter, and what's being tested is familiarity with a particular method (and an inferior method).

So the kids whose parents successfully just fucking teach their kids math at home are being intentionally disempowered in order to make sure that only kids who have attended public schools and learned this bullshit nonsense method can do well.

That's why.

[The Late P Brooks]

What are children for, if not experimentation by Top Men, for the Greater Good?
Especially twins.

[Juice]

http://www.youtube.com/watch?v=GVqoYvlEZis

[Edwood]

The child is starting to learn algebra while learning division. This will pay off in the future. So far I don't see what all the fuss is about.

[anon]

But the child isn't actually "learning" algebra. S/he's learning to guess shit first, then see if it worked, and then repeat the whole process if it didn't...

So rather than finding the correct answer to the posited problem, she's being trained to be a government employee. "Ah, fuck it, the right answer doesn't matter, we'll just try again if we're wrong."

[Zeb]

It's really not guessing. As someone points out above, it's really just a more explicit way of doing long division.

Even if it were, guess and check is a perfectly valid, and sometimes reasonably efficient way to solve problems.

[Stormy Dragon]

Heck, guess and check essentially is the scientific process. They just call them hypotheses instead of guesses.

[Brandon]

Do they get budget increases if they're wrong?

[DaveSs]

There isn't a guess going on.
The method here is to find multiples of 10, 100, 1000, and so on to subtract off the dividend, allegedly to 'simplify' the problem. Multiples of 10 can of course be easily done in your head.

Because 84 is less than 100, you would be looking for a multiple of 10 that is also divisible by your divisor (7) which is of course, 70
84-70 = 14

For something like 84 / 3
84-(3*10)= 54
54-(3*10) = 24
Since 24 is less than 30 there are no more multiples of 10 to use, so you must do the division.
24 / 3 = 8
Then add that to everything you had to multiply.
10 + 10 + 8 = 28

My explanation might not be 100% the same as the way its being taught, but I'm sure its fairly close.

Personally I don't see whats so complicated about long division.

[Agile Cyborg]

Personally I don't see whats so complicated about long division.

Because anything with more numbers must mean less time to climb trees and catch caterpillars.

[Brandon]

You're mixing up your straw men.

[MegaloMonocle]

The child is starting to learn algebra while learning division.

Why not just teach her to do division, and then teach her to do algebra?

Why make the simpler operations unnecessarily complicated and hard to learn?

Does anyone think this is going to help kids engage with and learn math, or is it more likely to put them off math?

To me, this whole thing reeks of high-dollar consultants who have to justify their fee by making things look a lot harder than they are.

[Warren]

Because this is better.

[Brandon]

Unsupported assertion.

[Rasilio]

Because once you get past 8th or 9th grade nobody expects you to be solving 2386/415 in your head anymore, there are calculators for that. Wasting time teaching a method which is utterly useless in the real world and provides no other benefit of greater understanding of the underlying laws of mathematics is just that, a waste of time.

Sort of like those moron schools that still teach cursive classes.

[tarran]

Teaching elementary school children that math consists of makework and is to be avoided is *better*?

[Square]

Ironically, the theory was meant to combat the effect of school making children hate learning by making the content more tailored to the individual capabilities of the child.

[The Last American Hero]

Ironically, Obamacare was supposed to lower the cost of health care. Ironically, the minimum wage was supposed to make life better for the inexperienced/hard to employ.
Ironically, communism was supposed to create a just, prosperous, egalitarian society...

[Bobarian (dinosaur hunter)]

Threadwinner!

[The Late P Brooks]

the kids caught in the transition years will have been undeniably ill-served.

The world needs ditch diggers, too.

[The Late P Brooks]

84/7= (33+51)/7

See how easy it is?

[Warren]

Yes I do, but you don't. You get an F.

[Bobarian (dinosaur hunter)]

If you cut off three of your fingers, it'll get a lot easier to start thinking in base 7 math.

[Warren]

Just because a certain way of learning is confusing for parents doesn't make it inherently bad, of course.
That's true.

It's perfectly possible for educators to invent an approach that makes math easier for kids, even if older generations don't get it.
No your not getting it. It's not about making "math easier". If you wanted to make arithmetic easier, you'd just show the kid how to use the calculator app on his phone. It's about preparing the kid for more advanced math concepts that will actually be useful in the coming years.

As opposed to having to unlearn everything you learned in K-8 when you started taking trig and calc. You know, the way generations of STEM students had to do because our K-8 public school teachers never took trig or calc and couldn't give a shit anyway just so long as they could get the slowest kids to count on their fingers and pass them along.

[robc]

Who had to unlearn everything K-8 when they took trig and calculus?

Im fine with variable approaches, but the old way didnt teach anything that had to be unlearned.

There is nothing wrong with some of the grouping methods being taught, but it shouldnt be the primary method being taught.

Memorization of basic tables and long division above those should be the primary methods, with grouping being an alternate that helps in certain situations.

[Warren]

Memorization of basic tables and long division above those should be the primary methods, with grouping being an alternate that helps in certain situations.

Oh hells no. Memorizing tables and long division is probably the worst possible method. I'd sooner teach my kid to use a slide rule than do long division.

[anon]

So what you're saying is your kid is effectively retarded?

[Brandon]

Not the kid, necessarily.

[Zeb]

I'd have kids learn all of those things.

Long division is great. I even use it occasionally if I don't have a calculator to hand. Slide rules are also great way to get an intuitive sense of why logarithms are interesting, though they aren't terribly practical anymore.

[Bryan C]

Memorization is a really, really useful skill. I really wish I'd been required to do more of it.

[Zeb]

This is true too. And it is a skill that you learn.

[Stormy Dragon]

Memorization is becoming an increasingly less useful skill each year. In a world where nearly all human knowledge is instaneously avaialble on a small box in your shirt pocket, ndexing (knowing where and how to find information quickly) is more important than memorization.

[Mickey Rat]

Not for understanding mathematics.

[Acosmist]

Very few people can do advanced math. And that means algebra I.

[Brandon]

What the fuck are you talking about? Math is math. Calculus and trig are more complex, but if you couldn't do arithmetic you couldn't do algebra, and if you couldn't do algebra you were fucked for calculus.

[Warren]

No, you need to understand addition to do algebra, but you don't need to be able to do it. There are concepts of numbers and operators that get discarded when focusing on the mechanics of finding the answer to simple arithmetic problems. The CC method focuses on those concepts.

[anon]

No, you need to understand addition to do algebra, but you don't need to be able to do it.

If you aren't able to "do it," then you don't understand it.

[Brandon]

We can tell when someone is just repeating talking points.

[fuck you Belinda Carlisle]

"you need to understand addition to do algebra, but you don't need to be able to do it. "

When I tried that on my algebra teacher, she failed me for not showing my work.

[fuck you Belinda Carlisle]

"Just because a certain way of learning is confusing for parents doesn't make it inherently bad, of course. It's perfectly possible for educators to invent an approach that makes math easier for kids, even if older generations don't get it."

No, that's not fucking true.

Parents are supposed to be a part of the education process, and if your method doesn't at least take them into consideration, it is a fail from the start.

I read the author asserting this too, and frankly, your attitudes are a large part of why schools are so fucked up.

[trshmnster the terrible]

^this. Then, out the other side of their mouth, they bitch about the absentee parents and their delinquent kids.

[robc]

You still need to know the basic tables to get to the groupings of 70.

You have to know that 7x10=70 and 7x2=14 to start. Since they have already memorized the tables to get that far, why do the groupings instead of long division?

[OldMexican]

Re: robc,

You have to know that 7x10=70 and 7x2=14 to start. Since they have already memorized the tables to get that far, why do the groupings instead of long division?

Some here have commented that the purpose is to prepare kids for algebra. Which makes me think that the REAL reason Common Core is trying to cram factorization in elementary school is because middle school math teachers can't do algebra. Get 'em while they're young.

[tarran]

In Turkey, they start algebra in 4th grade. They don't do this bullshit.

[Brandon]

Then why don't you move to Somalia Turkey?

[The Late P Brooks]

I've said it a jillion times, so-called "education experts" should be looking for ways to efficiently diversify learning models, not make everyone learn the same way.

Yeah, well, nobody listens to you because you're crazy.

[Kaptious Kristen]

I know. I expect "them" to come for me any day now.

[OldMexican]

Just because a certain way of learning is confusing for parents doesn't make it inherently bad, of course

No, it makes it inherently confusing.

It's perfectly possible for educators to invent an approach that makes math easier for kids, even if older generations don't get it.

It is more likely, however, that someone is trying to confuse the heck out of kids AND parents so that kids lose confidence in their parents' abilities.

Just sayin'.

[tarran]

To everyone who doesn't see the big deal, let me explain it to you.

Common Core is teaching my daughter to hate math.

My daughter is brilliant, and she will do well in Math. She is numerate, and even understands basic algebra despite being in 4th grade.

And she hates math because of bullshit math assignments like this. To her, she is being punished with make work after she finds the answer. She is not even 10 yet, and these exercises strike her not as useful practice but as unnecessary make work. When she is told she has to solve the same problem three different ways, she doesn't cheer; she gets pissed because the extra work is cutting into her tree climbing and butterfly rescuing time.

She is considered gifted in math, started school interested in it, and it takes all my dad-fu to maintain that interest in the face of do gooders trying to "improve" her.

[robc]

When she is told she has to solve the same problem three different ways, she doesn't cheer; she gets pissed because the extra work is cutting into her tree climbing and butterfly rescuing time.

Also this. See my 1:29 comment for an example at a top STEM school.

People solve problems differently. Having to do it n different ways is stupid, if you have a method that works.

[Agile Cyborg]

Homework beyond 15-20 minutes total should be rejected by all school boards. However, how can she hate math at such a young age due to 'strenuous aspects' unless someone informs her there exists a 'better' way? I wonder if parents are unduly and unintentionally leading their kids into frustration rather than simply giving the newer style of math a shot. I say this as someone who understands the frustrations of parents in this regard. I've there right now as a matter of fact with my 10 year-old.

I think all parents should attempt to read Bertrand Russell's Introduction to Mathematical Philosophy just so they realize just how complex even simple mathematics really can be. Might open their minds a bit to alternative approaches.

[tarran]

No. It's because frequently they ask her to solve the same problem in three different ways.

It's one thing to expose kids to a bunch of different approaches and let them gravitate towards the approach that most suits the way their minds work.

But that's not happening here. She gets the right answer, then has to get it a different way, and then yet another way.

Compounding the mess, the people preparing the homework assignments use the correct terminology with any precision. Rather than using words like 'expression' and 'equation' they use sloppy lossely-defined terms, like 'math sentence' and the kid is often helpless because none of the adults are sure what these terms mean. When I google the terms, I am hoping that the explanations I read happen to be the same ones the teachers had in mind when they selected the assignment. I've been burned a couple of times because the meaning the teacher had and the meaning I found on the web differed significantly.

All of this makes her think that what she is being taught is a bullshit waste of time, since (a) it's unnecessary work, and (b) I taught math at the college level and *I* don't know it implying it's unnecessary knowledge.

The good news is that the insanity really peaked at grades 2 and 3 and are getting less and less as the material regresses towards the traditional things an incoming college student is supposed to know.

[fuck you Belinda Carlisle]

"It's one thing to expose kids to a bunch of different approaches and let them gravitate towards the approach that most suits the way their minds work.

But that's not happening here. She gets the right answer, then has to get it a different way, and then yet another way."

Well, not to question your dad-fu, but finding the answer isn't the work there, reconstituting the problem is, so while it's nice she has found A solution, finding A solution isn't the assignment.

[Bobarian (dinosaur hunter)]

Make work.

Fuck that with a rusty bowie knife.

[Cyto]

I had real problems doing "make work" assignments in school. Our chemistry teacher had us write out all the electrons in all the orbitals for all of the elements in the periodic table. I couldn't do it.

I don't mean I was not able to understand the assignment. Or that I was not able to do the writing, or get all the answers right. I mean I was not able to bring myself to spend hours writing out all of that meaningless detail when getting through the first row of transition metals pretty much sets the pattern for the whole thing.

My son is already starting to pick up on the same issues with this common core math. I have been explaining to him that they are trying to teach him more than just how to get the answer "12", but it all just feels like meaningless make-work to him.

They have him doing "math sentences" like Taran described. So he has to read a word problem. Discern that 7+5 will give him the proper result. Do 7+5 to get 12. Then write 7+5=12. Then write "Seven Plus Five Equal Twelve". Then draw seven boxes and five boxes and then a stack of ten boxes and two boxes. Then he writes "12" in the space for the answer.

I was jaded by the mind-numbing monotony of school by the time I hit 10th grade. All of the busy work made mustering the energy to do homework extremely difficult and left me ill-prepared for the work load in college. It looks like they have managed to push this phenomenon into grade school.

[Curt]

To phrase fyBC's comments slightly differently, the point of these lessons isn't for your daughter to "find the answer", the point is for her to learn different ways to find that answer and become proficient at each of those methods. Maybe she currently likes using Method #1 most and that's great when her math problems are simple. But when those math problems become more complex, she'll need to know several methods, be able to determine which is best for the situation, and be proficient at using it.

You said that she's brilliant. I have no reason to dispute that. But if she is, then she should be able to understand that her math problems are going to get increasingly more complex and sometimes her preferred approach will be difficult to use.

Also, if she really is brilliant, then unfortunately she needs to prepare for about 9 more years of tremendous frustration with a school system that teaches to the lowest common denominator. This is just the tip of the iceberg compared to what lies ahead. Several of the math classes that I took through elementary/high school almost broke me. I would understand a concept in 5 minutes, but had to tolerate the next 50 minutes of the teacher repeating to the rest of the class. Best solution I found was getting the teacher to tell me the night's homework assignment at start of class. Then, I could do it while she continued teaching everyone. Helped free up afternoons & evenings. Not sure if she can get away with that in 4th grade.

[MegaloMonocle]

Common Core is teaching my daughter to hate math.

Which is my point above.

Why make the simpler operations unnecessarily complicated and hard to learn?

Does anyone think this is going to help kids engage with and learn math, or is it more likely to put them off math?

[Zeb]

That is the problem. I don't think that the method here is completely useless. But forcing kids who understand things to do the stupid busy work does those kids a great disservice. And since most of the teachers probably don't understand the underlying concepts, stupid busy work is likely to be how it ends up. One of the worst, most harmful things that schools do is to force smart kids to stay with the rest of the class even if they get nothing from it. But I guess putting the smart kids in a class that is at their level is unfair or something.

[Square]

This has always been the case, though.

I'm a classic example, myself - math always came very easily to me, and faced with a page of 45 iterations of the same damn problem, I would write the answers (since they were all obvious) and go about my business, getting an F because I didn't show my work.

By Freshman year of high school I was being held back, because despite getting consistently 95% or higher on the tests, I didn't show work and I didn't do homework.

So I wound up taking the same classes over and over and by the time I got to college I was so catastrophically far behind on the math track that engineering and hard sciences were simply not an option.

The research that went into these new methods were intended to prevent EXACTLY what happened to me.

Something got lost on the way to implementation, though, and now I have just the same arguments with my mathematically inclined daughter that my parents had with me - "I know it's stupid and it drives you crazy, but you HAVE to do it. . ."

[tarran]

That's because you had bad teachers who didn't care enough to educate you.

And no amount of curriculum tweaking can fix the problem of bad teachers.

[Fluffy]

Where were your parents?

I would be the fucking angel of death in that situation.

I am waiting with my finger on the Warty button for the first fucking time anyone tries to give my kid a bad grade when he got the right answer.

Because FUCK YOU THE CORRECT ANSWER IS THE ONLY MOTHERFUCKING GOAL ALWAYS AND EVERYWHERE.

[Square]

My parents chose it as an opportunity lesson in the stupidity of government and authority figures generally speaking. Neither of them did well in school, either, and were un-shocked when I dropped out.

[Every Cop is a Criminal]

I'm a classic example, myself - math always came very easily to me, and faced with a page of 45 iterations of the same damn problem, I would write the answers (since they were all obvious) and go about my business, getting an F because I didn't show my work.

Very similar here. In second year algebra, I took the final and showed no work. I got every one right. Turns out, someone had stolen the test answers, so the teacher accused me of cheating. I said I didn't cheat, so he wrote several problems on the blackboard and told me to solve them without showing any work. Nailed them all, so he gave me an A. To his credit, at least he gave me a chance to exonerate myself of the cheating charge.

[antisocial-ist]

My daughter is the type of kid that's very interested in learning something the first time, apathetic the second time, and bored out of her skull by the third time. She comes by it honestly, but I'm very glad we got her in a private school and she won't have to deal with this and other bullshit like I had to in school.

[OldMexican]

I learned long division in Primary (i.e. Elementary) school.

I learned Algebra in Secondary (i.e. Middle school to Junior High) school.

I perfectly understood Algebra without having to learn to do division the way it is shown above.

But then again, I didn't go through the Amerikan Pulbic Skool Seistem Dat Teeches Kidz To Red An Writ - I went to private school in Mexico.

Sucks to be you.

[Zeb]

Yeah, and it's good to be you.

But the fact is that lots of kids get to algebra and just shut down. I certainly don't think that this is how every kid needs to learn things so that they can do algebra later. But it might help some. As usual, the problem goes away when you stop putting government in charge of the schools and let people find what actually works well for them.

[Kaptious Kristen]

I shut down in algebra in 8th grade. Took it again in 9th grade and aced it. L learned nothing new between 8th and 9th grades. I attribute it to my brain's reasoning abilities finally kicking in.

[DaveSs]

Part of the difficulty us adults have with this method is that its different than how we were taught.

We learned long division and multiplication tables. That to us is 'easy'
There's always more than one way to solve a problem.

Many of these 'new' methods aren't actually new. Often have been taught for centuries in other cultures.

[anon]

Often have been taught for centuries in other cultures.

Right, and we all know other cultures do things better!

Have you ever visited any country outside US/Canada?

Protip: They're all shit.

[DaveSs]

I've spent a grand total of 2 hours outside These United States

I'm not saying these methods are better.

Point was two part:
First, our brains have been trained over decades to use the methods we were taught, so every other method appears clumsy and complicated.

And second, that these methods aren't some magical mystical new-math thing that some douchebag at DOE thought up to confuse parents and corrupt the yutes. These methods have been successfully used to teach some of the worlds geniuses in math.

[Agile Cyborg]

Often have been taught for centuries in other cultures.

And probably where the world's best computer hackers reside, i.e., people who are so comfortable with machine language they can break machines with it.

[fuck you Belinda Carlisle]

Oh shut the fuck up.

[An Innocent Man]

I'm mostly annoyed by the idea that everyone learns at the same pace, at the same level. In 4th grade you should know x,y,z. If you're in 4th and not ready for x,y,z, we are going to send you along to 5th anyhow cause just because. And if you're in 3rd and above average and already know x,y,z you can't move on cause you gotta wait on everyone else. So just sit there and stare into space. So the slow learner and the fast learner both get discouraged and give up.

[Square]

My second-grade daughter was recently tested on how to spell "dog." She's already read the Hobbit probably six times, and she's four books into Harry Potter.

[Somalian Road Corporation]

Better that everyone be equally miserable and held back, because inequality is like, evil and stuff.

[trshmnster the terrible]

Yep, add into it a fear of authority, and you have the makings of me. I was reading at a 5th grade level in kindergarten. A ninth grade level in 2nd grade. I could multiply and divide when other kids couldn't add or subtract.

However, after 4 years of utter boredom, middle school was really hard. I hated school so much that I didn't do homework or participate. I dunno how many projects and papers I turned in late or not at all.

I really didn't like learning again until 12th grade, all because the system was built to the average kid.

Part of the problem is the curriculum, but most of the problem is the system. Common Core sucks because it promotes this bad system, not necessarily because it does things differently than we learned it.

[Cyto]

I had the same issues. I distinctly remember getting in trouble the first day of school in 3rd grade. While the teacher was explaining how our new math workbook was going to work, I was enjoying solving all the math problems. As I was finishing the book, the kid next to me told the teacher I was working ahead.

So I finished 9 weeks worth of math in about 10 minutes. And I got in trouble for not paying attention. Nobody noticed that maybe I shouldn't be working at that level and needed more attention. So I spent the next few years learning to work at the same pace as everyone else. Not a useful skill outside of the assembly line.

Later I learned that the entire point of the US public education system was precisely to prepare workers for the assembly line. So I suppose on that level they are a success.

[Spartacus]

Still relevant.

[An Innocent Man]

No workie linkie.

[kinnath]

The common core standards are pretty straightforward even though they demand too much too soon.

The problems associated with common core (in no particular order) are:

- Crony capitalism controls the production of teaching materials and testing systems

- The public education system has become the primary means of marketing of progress ideals

- The number of teachers that teach math who have any relevant degree in math is vanishingly small

[Derpetologist]

For public schools, the method that should be taught first and mainly is the one that is the easiest for most people. That generally means the method that requires the fewest number of steps.

I think it would be better to give students a table and a bunch of multiplication problems. Once they've used it enough times, they'll have it memorized automatically. In fact, I favor this approach for teaching all basic arithmetic.

Most people can remember 3 x 4 = 12 more easily than they can remember the process for getting there.

[fuck you Belinda Carlisle]

"Just because a certain way of learning is confusing for parents doesn't make it inherently bad, of course. It's perfectly possible for educators to invent an approach that makes math easier for kids, even if older generations don't get it."

I posted a response to this above as well, this is fucking stupid and wrong.

If you want parents involved, you don't design your system in a way that excludes them.

[Notorious G.K.C.]

Stick the pig in at one end, and if tasty sausage comes out, that should be enough.

IOW, give the kids a timed test, and if they get the right answers on the questions within the time given - without cheating - then assume they have mastered the material.

[DaveSs]

I'm reminded of a disparaging comment on 'new math' that a much older relative made.
The problem was 32 - 12, and the solution was written like this.

12 + 3 = 15
15 + 5 = 20
20 + 10 = 30
30 + 2 = 32
3 + 5 + 10 + 2 = 20

In truth, its not all that much different than how people used to count change.
Nowadays they just hand you your change, but before adding machines they would count out the change. (Something I would expect an old person to remember)

$3.78 is the bill, and you give the cashier a $5 bill.
So our math problem is 5 - 3.78

3.78 + 0.01 = 3.79
3.79 + 0.01 = 3.80
3.80 + 0.10 = 3.90
3.90 + 0.10 = 4.00
4.00 + 1.00 = 5.00
1 + .1 + .1 + .01 + .01 = 1.22

[Old Man With Candy]

Ugh, just finished a contentious phone call with my kid's math teacher. He's failing despite being naturally gifted at match. If you ask him to multiply (say) two 3-digit numbers, he closes his eyes for a couple of seconds and tells you the answer. And it's correct. That is unacceptable at his school.

I once made the mistake of asking him how he does it. "I just imagine that there's a dollar sign in front of the numbers and then I can just see what the answer is." A true libertarian in the making.

I had him doing quadratics in his head three years ago and the fucking school has him doing arithmetic busy-work. The teacher is not a bright woman and knows very little about actual math.

[Cyto]

He should hang out with my Dad. When I was in school he used to quiz me with those sorts of problems. "What is 456 * 1245? Quick!" A chemical engineer and rocket scientist who had the freak ability to multiply 4 digit numbers in his head quicker than you could put them in a calculator, he had a hard time understanding that this is not normal. He always said "the mind is a muscle, you have to exercise it to get better!" He was convinced that the only reason I couldn't do it was general sloth.

[Mickey Rat]

My Dad did something similar to me. We'd be running errands in the car and all of a sudden it was math pop quiz time.

[scott777]

check out Saxon Math author Stephen Hake's 3 part series on Common Core. I think it provides a unique perspective on this topic.

http://wp.me/p4nApj-1j

[Restoring the Dream]

You learn reading by reading. You learn math by playing with numbers. When you go through multiplication tables and notice the patterns, you are getting the intuition that math requires. You need those aha experiences like little easter eggs to keep going. So few teachers understand the joy or excitement of mathematics, they certainly cannot teach it. Mathematics is all about discovery in a way that languages cannot be, because math is logical. The thrill of discovery is the best part of math. There's hardly anything better than the moment when you figure out,"Holy crap! you can use this to figure out THIS!"

[Zeb]

I just whip out my tape measure and see that 7' and 84" coincide.

[robc]

I got pissed at a TA over that comment my freshman year.

It was a "fine the point this line intersects this plane".

It was obvious, it was something like (1,5,0). I mean, come on, it had a fucking zero in it.

He orginally gave me zero credit. I complained, he said that I didnt show any work. I said I didnt do any work because it was obvious.

I did get partial credit at that point.

[UnCivilServant]

Show your work, smart-guy.

What the image appears to be trying to teach is the mental math developed after rote and long division have been mastered. While it resembled what went on in my head when I processed the question, trying to teach that is outright absurd.

But showing the long division work (the qay I was taught):

8/7 is 1 remainder 1 - add the decimal location of the dividend to give 10.

14/7 is 2 remainder 0

10 + 2 is 12.

[anon]

Well played.

[MegaloMonocle]

That may be the first comment on H & R ever that began with "I just whip out my . . . ." and ends on a, err, family-friendly note.

[kinnath]

. . . big 12 inch . . .

[anon]

To be fair, I thought he wrote "I just whip out my dick..." before I commented.

[Muzzle of Bees]

"the qay..."

Is this like the gender-neutral form of way?

[Restoring the Dream]

Precisely- they're trying to teach intuition, which can't be done, as far as I'm concerned. It comes from letting your mind wander around in the numbers as you memorize multiplication tables.(68-69,4th grade- up to 18 times 18)
Best thing I ever did.

[UnCivilServant]

It's a typographic error. Typing wasn't a subject until high school, by then I was hopeless with a keyboard.

[Zeb]

I loved it when I got to the point in college math where you could get away with just writing "obvious" instead of explicitly proving certain things.

[Zeb]

My dick isn't quite 7' long.

[Bobarian (dinosaur hunter)]

That's pretty qay.