Pull Your Hair Out As You Learn the Common Core Way of Doing 6 + 10

They might be overthinking this.

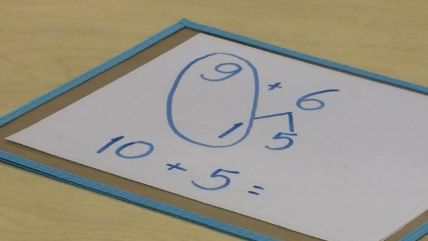
Parents in New York are having trouble helping their kids with math homework now that the curriculum is aligned to the national Common Core standards, so a local news channel has released some videos explaining the new lessons.

Ready to pull your hair out? Here's the fancy pants new way of figuring out 9 + 6:

Instead of just, well, adding 9 and 6, students must run a gauntlet of extra addition, "decomposing" 6 into 1 and 5, "anchoring" 9 to 1 to make 10, and then adding the leftover 5. The new way requires a lot more time, a higher vocabulary, and more work. But it's somehow supposed to be "more comfortable" for young learners, in the estimation of standards peddlers.

How parents must long for the good old days of rote memorization! (Incidentally, a recent Stanford University study found that rote memorization is important for developing brains.)

The videos also illustrate why adapting to Core-aligned curriculum is a difficult—and expensive—process for schools. New instructional materials must be purchased, teachers retrained, tests rewritten, etc.

Read more from Reason on Common Core here.

Hat tip: Eric Owen / The Daily Caller

Comments

[Almanian!]

This New Math? is so....new

[Derpetologist]

Does anyone think it's odd that the people with the lowest SAT scores are put in charge of teaching?

http://platedlizard.blogspot.c.....-shut.html

[Arcxjo]

Only because anyone smart enough to find the SAT room is automatically barred from being a cop.

[buybuydandavis]

What is not surprising is that those who can't do take a job where there is value in being smarter than a third grader, and once you're in, you can't be fired, no matter how ignorant and incompetent you are.

[KWebb]

So it's a jargon filled way of saying that 9+X == 10+(X-1)?

[MegaloMonocle]

Why do addition, when you can do algebra instead?

[JWW]

What, are you just trying to confuse the poor kids?!? They need to decompose the 6 and then partner nine with one and ..... yeah, fuck it, what you said.

[robc]

Here is the thing. "Decomposing" is subtraction.

Why teach subtraction before they have a handle on basic addition.

They need to know 9+6 before they start considering 6-1 and 10-9.

Think about what they are asking.

1. Make the 9 into a 10. What is 10-9? 1
2. Subtract that 1 from the 6. What is 6-1? 5
3. Now add 10+5.

Two subtractions to get to an addition.

[robc]

Correction: Two subtractions to get to a slightly easier addition.

What the fuck?

[HazelMeade]

well, if you visualize the 9 as a group of 9 objects and the 6 as a group of 6 objects, then it's pretty easy to "move" the one object to the other pile in your head.

[robc]

Yes, but to know how many objects to move is subtraction.

[Spencer]

It's even easier just to move ALL 6 items over to the pile of nine and get 15...

[robc]

Especially if you arrange both piles in your head in rows of 3.

But now that is multiplication.

So, instead of subtraction, lets teach multiplication first!!!

[HazelMeade]

Well, it would be fun you have a class where you do all of those things. Just imagine all the numbers as piles and see how many different ways you can come up with of ending up with 15.

[robc]

Why do you need a class?

I did that kind of shit for fun. And still do, although at a higher level.

[CatoTheElder]

^THIS!

[goneGalt]

Uhhh...

This nine plus six equals (shift a one) ten plus five is precisely how I "memorized" my addition tables at six years old during the time of the Cuban Missile Crisis.

Full Disclosure: They were already teaching us commutative and associative properties of addition in the first grade in those days.

Thing is, if I could figure this out all by my six year old self, what do we need these Ph.D types in the DofEd?

[Solomon Grundy]

That works fine as a shortcut for 9+6, what about 7+6? They're going to have to understand subtraction to do it that way.

[goneGalt]

Oh, I agree about the understanding part, sort of. I'm just saying that is how it worked in my mind... 7 + 6 would be 7 + 3 + 3... at six years old.

It helped that the teacher would grab a bunch of pencils and shift them back and forth on the table in differing groups. I never really saw it as "knowing" subtraction or "memorizing" certain answers. Numbers were always something I could visualize. And they made sense to me somehow.

Interestingly, I never really gave it any thought until this discussion!

[Bill]

THis seems like a perfectly reasonable way of getting children to understand why 9+6=15 or 7+6 = 13.

There is still plenty of room for memorizing in addition to showing them why it works.

Conservatives may be barking up the wrong tree on this one. Now whether you need federal rules for all this is a different question.

[Suicidy]

This all smacks if White Privelge.

[Arcxjo]

Well, two wrongs make a right.

[BohdanUke1]

Toooooooo funny! Kudos!

[BohdanUke1]

Toooooo Funny...

[MegaloMonocle]

a recent Stanford University study found that rote memorization is important for developing brains

So all those Wahhabi madrassas, where memorizing Koranic texts is pretty much the curriculum, must be cranking frickin' geniuses by the busload.

[Brandon]

They've managed to destroy a Constitutional republic in about a decade, they can't be too dumb.

[RussianPrimeMinister]

That's so brutally correct.

[avocats]

No, at some point the brain needs to begin analyzing. That's not allowed in fundamentalist religions.

[Restoras]

Fucking stupid.

[Obama's Buttplug]

It's not just common core. 10 years ago, 5th graders I know were being taught long division through a complex process called "adding up".

[thom]

I learned long division doing something like this. My dad told me that division is nothing more than repeated subtraction, so I started just subtracting the denominator from the numerator over and over again and tallying each time. This actually was enough for a few years of elementary school math, but eventually I had to learn to do it the proper way.

[Rob]

My brother was taught the "adding up" method. He still can't do long division on in his head, or on paper.

I learned the "rote" way with flash cards and had to memorize everything from 0*0 to 12*12. After that I never had a problem with math until I hit calculus, and the problem there probably had more to do with skipping class than anything else.

[robc]

Its fucking stupid for young learners and for x+y where x and y are single digits.

They should memorize the tables.

However, this is how I add up stuff in my head all the time. If Im adding 143 and 557, the first thing Im doing is making it 200+500.

[JWW]

Sure you do that. I make it 150 + 550

:-p

[robc]

If it was 143 and 567, sure, go to 150+560, but when you see the obvious 43 and 57, why not go an extra digit?

[MegaloMonocle]

Umm, the 57 isn't obvious to me. I don't see it in either 143 or 567.

[HazelMeade]

I think he means 557.

[robc]

Look at my 5:52 post.

[plusafdotcom]

Actually, you skipped 100 plus 100 plus 500 step...

I memorized the multiplication tables from 1x1 to 9x12 because I'm more "visual" in terms of learning, and having those answers stuck in my head, about 60 years later, now, lets me do a lot of multiplication, division and fractions 'in my head' without all the other New Math gingerbread involved.

Now, someone tell me that all the New Math 'unions and intersections' helps THEM figure out things on a daily basis when they go to the supermarket...

🙂

[Being Waterboarded]

Precisely this ^. There is room for both rote memorization (anything single digits for sure) and a method by which rounding is used to make a simple addition, followed by corrections (addition or subtraction) based on the rounding that takes place.

Teach the rote memorization first. Then, when working with large numbers, you can teach the rounding method.

[avocats]

Exactly. But that doesn't allow for rolling out "new" methods and textbooks and training sessions for school districts to pay for every five years.

[Pope Jimbo]

I had an 8th grade teacher who spent half a year teaching us how to do the folowing:

Fast Estimates (addition/subtraction)
Fast estimates of percentages
All the squares from 1 to 25
Convert fractions to decimals (to 2 places)
Fast estimates of number to fractions

All his drills were based as much on speed as on accuracy. I went on to get a degree in electrical engineering and all the math that entails, but I still think that 8th grade class as one of the most useful I ever had.

[PapayaSF]

Wow, good teacher.

[avocats]

If the tests are asking for estimates, rather than exact answers.
I think all those hacks are important for 8th graders. Problem is that these are younger kids.

[John]

I forget where I saw it but there was a guy with a advanced engineering degree who could not figure out how to do his 5th grader son's new "common core" math problem.

This shit is beyond retarded. I think what is going on here is the idea is to grade based on gender and race. Make sure the right groups get the good grades and the evil boys and especially white boys get the worst grades. One way to do that is create problems that no on in their right mind could do the way they are expected to be done. If everyone is wrong, then the teacher can arbitrarily decide who is "right".

[PapayaSF]

I think there's also some "created by a committee" aspect in CC. Start with some (questionable) education school theories, run them through a bunch of committees and editors, and in the end you may get something that doesn't even make sense.

The basic idea behind CC isn't that objectionable, but as usual bureaucracies mess things up.

[The Late P Brooks]

FUCK YOU AND THE AUTOPLAY VIDEO YOU RODE IN ON.

[robc]

Autoplay is worse than Nicole and Hitler combined.

[Spencer]

Ok, now if you're adding Nicole and Hitler, make sure you break down Hitler into Personal Antisemitism + Destroyed German Economy after unfair resolution of WW1. Then take nicole and pair that with Personal Antisemitism...

[MegaloMonocle]

As a bonus, Hitler is already decomposed.

[thom]

Autoplay is worse than Hitler if Hitler traveled in coach and reclined his seat.

[avocats]

Thanks, you guys. Always a pleasure. 🙂

[plusafdotcom]

^That!

[Zeb]

Yes. Please stop posting autoplaying videos, Reason.

[Robby Soave]

It wasn't intentional, and I can't figure out how to turn it off.

[Zeb]

Some sites seem to just do it. It is often a problem with Daily SHow clips and some others, it seems.

[Ted S.]

Set your browser to show plug-ins only on demand.

[Jayburd]

Hey Robbie, how's Rico?

[HazelMeade]

Word. Every time I make a comment it reloads.

[HazelMeade]

FUCK! Not again!!!

[HazelMeade]

FUUUUUUUUCK!!!!!!!!!!!!!!!!!!!!!!!!

[Spencer]

Is 10+5 intrinsically easier than 9+6? IF so, 1) why? and 2) is it SO MUCH intrinsically easier as to add the difficulty of breaking down numbers and re adding them?

I mean, is 9+6 harder than 6-1 (to get the 5 and the 1)?

What SCIENCE is this based on?!

[robc]

See my comment above.

Exactly. And its not 1 subtraction, it is two. Two subtractions cannot possibly be easier than the difference between the two different additions.

[Spencer]

My comment might be lower, but it was first. Therefore I'm suing you over the theft of my intellectual property!

[robc]

You realize I oppose IP right?

[Spencer]

then you should have no problem admitting that you stole it in violation of knowing what it is.

[Vulgar Madman]

All you need to know is that it's SCIENCE!
SCIENCE is mysterious and unknowable, and cannot be questioned!

[Heroic Mulatto]

Is 10+5 intrinsically easier than 9+6?

Yes.

IF so, 1) why?

The brain more easily subitizes 10 into two groups of 5 than 9 into 3 groups of 3 and 6 into 2 groups of three.

2) is it SO MUCH intrinsically easier as to add the difficulty of breaking down numbers and re adding them?

The point isn't ease of calculation.You can't get easier than just memorizing "9 + 6 = 15". The point is getting children to understand how math "works".

Now one could debate whether or not it's developmentally appropriate for 1st graders to delve into such topics, but no one is saying that the kids are being taught to salve the equations that way because it is quicker, nor is anyone suggesting that this is they way they will continue to solve problems once they understand the mechanics behind it.

What SCIENCE is this based on?!

I would guess you could find that answer here.

[Redmanfms]

You can't get easier than just memorizing "9 + 6 = 15".

Which is why you teach it that way to grade schoolers.

GRADE SCHOOLERS.

The point is getting children to understand how math "works".

Algebra.

[Spencer]

"captures a feeling of immediately knowing how many items lie within the visual scene,"

I don't think this talks about 10 being better than any other numbers. In fact this is about recognizing how many items are in a group instantly upon seeing it- and how this ability degrades the larger the group gets. That's great if we're talking about estimating how many people are in a picture, etc. I might have missed it, but I didn't read the part about 10 being more easily subitized than 9 into 2 groups of 4.5... Also, the why's can come later. Kids can't get the why's always. Sometimes the why doesn't matter. In fact, WHY does 9 apples and 6 more apples = 15 apples? because IT DOES.

Your other link says nothing other than a basic abstract that illuminates no science.

[Heroic Mulatto]

Which is why you teach it that way to grade schoolers.

GRADE SCHOOLERS.

Well, the fact is most of Common Core math is actually a watered-down Singapore Math. Again, I'm no fan of the Common Core as I believe it is the next step in a Federal power play to destroy local control of school. Still, you want to know how math is taught in places like Japan, China, or Singapore? Well, that's how they teach their grade schoolers. They do it through "problem solving, analysis and discussion of multiple solution methods as well as errors, and a high level of rigor".

Now, one might not agree that the best strategy is to out-China China, Yong Zhao certainly doesn't. But the first step in defeating Common Core is to understand where they are coming from.

[Heroic Mulatto]

I don't think this talks about 10 being better than any other numbers.

I never said ten was "better", whatever that means. I said ten is quicker to subitize into 2 fives than 6 and 9 into groups of three. For an explanation of why that is look on page 3 of this article.

I didn't read the part about 10 being more easily subitized than 9 into 2 groups of 4.5.

I don't know enough about the subitization of fractions to say whether that is or isn't true. It would be cool to explore, though!

Also, the why's can come later. Kids can't get the why's always.

I strongly disagree. But that's why I'm against Common Core and public education in general. People have different educational philosophies and there isn't a one-size-fits-all way to learn or teach.

Your other link says nothing other than a basic abstract that illuminates no science.

The point is, I can give you Mathematics Pedagogy 101 in 1500 characters or less. I pointed you to a resource that you could use if you wanted to investigate the claims more deeply. Whether or not you have the time or desire to is up to you. But you can't deny that it's out there.

[Heroic Mulatto]

*I can't

[NotAnotherSkippy]

The brain more easily subitizes 10 into two groups of 5 than 9 into 3 groups of 3 and 6 into 2 groups of three.

I don't understand why decomposing 10 (or 9 or 6) has anything to do with it. I don't think many would solve the problem by adding/multiplying the number of 3's or 5's.

You're right that 10+5 is easier than 9+6 to a base 10-thinking human, but that's because of base of the system. There are no carries in that case and the computation is just a substitution. The story would be different in base 8 or base 12. Or did you mean that 10 itself is just easier to subitize? That I'll buy.

The video makes mention of the concept of base, which is maybe what you're getting at and is valid. The "anchoring" is just bizarre terminology in my mind for an otherwise acceptable way of solving the problem.

[avocats]

Just the "subitizing" "decomposing" and "anchoring" makes it crazy for 2d graders.

[Robert]

I dig this method. It's like what I'd use when trying to minimize coin exchanges in making a purchase. Like, "What can be done to these figures to get them up or down to rounder, more convenient numbers?"

[Robert]

But what I'd really like is to kill the goddamn autoplay on that video!

[plusafdotcom]

"What SCIENCE is this based on?!"?

The "science" of somebody getting a thesis out of it, publishing a book and (unfortunately) having a lot of drones 'follow' that lead.

Follow the money.

[phandaal]

So it's more beneficial for a child to memorize number tables?

9 + 6 = 15 BECAUSE part of the number 6 goes to make the 9 a 10, leaving you with 5. If you can't figure out concepts like that, then you don't have much hope with higher math, because I can god-damn-guarantee you'll actually have to use critical thinking to solve any problem harder than Calc 2.

Remember: a broken clock is right twice a day. Not everything these people say is wrong just because they say it.

[robc]

So it's more beneficial for a child to memorize number tables?

Yes. This was discussed in a thread the other day. Also see link above.

Rote memorization actually has advantages.

[phandaal]

Well good luck with math that you can't memorize, then.

[robc]

???

The purpose of rote memorization is to establish a foundation.

Once you have the foundation, you can move on.

This technique is fine at times, as Ive shown above. Did you even read the thread?

[phandaal]

Honestly I only skim the comments here, because y'all are some crazy m'fuckas.

So... No. I did not read your thesis.

Again, good luck with your castle in the clouds. You don't have a foundation if you memorize answers without understanding the fundamentals.

[robc]

The fundamentals are the memorization of the basic arithmetic tables.

Ive taken fucking insane amounts of higher level math (insane for an engineer, not for a math major). Memorization of basic arithmetic didnt set me back.

And read the link someone posted above. Memorization helps.

[phandaal]

My undergraduate degree is in Physics. We did enough math to get a minor just through the regular course loads. Trying to memorize higher math and THEN learn the fundamentals is just asking for failure.

Memorization may help the type of personality who becomes an Engineer, which is great! I like driving over bridges, so I'm glad that Engineers use tables of empirically-derived numbers.

[robc]

Who is talking about memorizing higher math?

Burn strawman burn.

I often derived equations on my dynamics tests, because I didnt memorize them. I understand knowing the reasoning behind things. But the ninesies can just be fucking memorized.

[phandaal]

The purpose of rote memorization is to establish a foundation.

Once you have the foundation, you can move on."

And then you talk about all the math you know. If it's true for lower math, it's true for higher math. Because when kids learn math in school it's the highest they've ever gone.

Yeah yeah strawman is the logical fallacy that the posters here learned. Congrats.

[robc]

If it's true for lower math, it's true for higher math.

No, no it isnt.

[phandaal]

Well, now we're just making assertions (myself included). I just wanted to add a dissenting voice to the circlejerk that these comments can sometimes become, and I have no intention of trying to convince you of anything.

[LessIsMore]

Tranlation: I'm not interested in substantiating my argument or making sense, or knowing the context of what's already been said, I just wanted to say something that was contrary to what others were saying.

Fuck off.

[CatoTheElder]

If it's true for lower math, it's true for higher math.

Not in my experience. The guys who try to memorize in diff e and stat end up dropping the class. But I never met anyone in a college math class who did not just know that 9+6=15.

[Spencer]

We're not saying we need to memorize all square roots of numbers and cosign for every function. That's a long way from saying it's easier and better to simply memorize that when you have 9 apples and you add 6 more apples you end up with 15 fucking apples.

[Spencer]

and I'm retarded and type things with the incorrect spelling.

[NotAnotherSkippy]

Memorization may help the type of personality who becomes an Engineer, which is great! I like driving over bridges, so I'm glad that Engineers use tables of empirically-derived numbers.

HAHAHAHAHAHAHAHAHAHAHA. Tell me again why it's useful to solve EVERYTHING in the time domain when the frequency domain turns soooooo many problems into simple multiplication. Are you seriously suggesting that you don't learn some rote techniques for solving, oh, say, diff eq's? Do you actually re-derive the erf(x) solution each time you need it? Do you actually do a delta-epsilon proof for d/dx(x^2)? And lest we forget: the spherical chicken!

[TCMann]

Wow, I never thought I would see a reference to the spherical chicken on this site. I had a physics teach in high school that just loved the spherical chicken.

[Brandon]

Wow, incorrect assertion, straw man, ad hominem, waaahh I'm leaving. That declined quickly.

[Solomon Grundy]

You don't have a foundation if you memorize answers without understanding the fundamentals.

The foundation is what you choose the foundation to be. Something people often forget about math and logic -- anything can be an axiom, the only caveat being that the choice of axioms will restrict what you can prove and/or disprove in that system.

If you take as your set of axioms the 36 products of numbers 1 thru 9, the property that zero times anything is zero, and the method of multiplying multi-digit numbers place by place, you have a system that is capable of handling multiplication of any set of nonnegative numbers. That's your foundation.

If you get beyond the bounds of this limited system, which 75% of people probably never will have reason to, you come back and reexamine the foundation, maybe build a deeper one based on the general distributive law. When you outgrow that one, come back and look at the field axioms and construction of the real numbers. That's how math actually developed in the human species.

[Red Rocks Rockin]

You don't have a foundation if you memorize answers without understanding the fundamentals.

The problem is that Common Core Math does not actually establish an understanding of the fundamentals--which, for decades consisted of memorizing the tables. The intuitive leaps in solving problems came about once kids gained a mastery in a memorization of those basic tables.

Common Core puts the cart before the horse. A bunch of bureaucrats noticed that people with advanced skills in math were making these intuitive leaps ahead of their peers, and presumed it was the shortcuts they'd figured out rather than the memorization that made them advanced. It presumes a memorized foundation isn't necessary if you knew "the tricks" for solving problems--except for the fact that the reason these kids were making the intuitive leaps is because they ALREADY had memorized the tables, and were taking the next step on their own in determining how to solve them in their head more quickly.

Common Core doesn't provide any sort of "understanding" of the fundamentals at all--it attempts to teach the tricks of math without the fundamentals firmly in place.

[avocats]

Exactly. Thank you.

[robc]

The point of the link being that you are more likely to figure out those critical thinking concepts if you memorize the number tables, because it developes your brain in some way we barely (if at all) understand.

Plus, two additional subtractions is a stupid way to do a single digit addition problem.

[phandaal]

I don't see any subtraction. I see 1 + 9 + 5 = 10 + 5 = 15

In any case, I'm saying that understanding the relationship between 9 and 10, and why when you add a number to 9 you get 10 plus that number minus 1, is more important than being able to memorize a number table.

[robc]

To know that 9 needs 1 more to make a set of 10, you have to subtract 9 from 10.

Generalize the problem. If its 8+6, now we need to add 8+2+4.

To know that we need to pull off 2, we subtract 8 from 10. Then we subtract 2 from 6. Now we can add 10 and 4.

Two subtractions in order to make the addition slightly easier.

[Juice]

I don't think the point is to make it easier.

[Spencer]

NO. No it's not. You don't see any subtraction? They have to subtract 5 from 6 to get to the 1. (or 1 from the 6 to get to the 5).

Then they have to know that 10-9 equals 1. So you've got to do 10-9 and 6-1 before you even start anything. Horrible.

[robc]

Im thinking anyone who doesnt see the 2 subtractions doesnt understand abstract math.

[Spencer]

I'm thinking they don't understand any math.

[phandaal]

Or you could just understand that 10 comes one number after 9. And you're not subtracting anything from the 6, you're just breaking it down into parts and adding those parts how you want.

[robc]

Breaking down into parts is exactly what subtraction is.

[MegaloMonocle]

Or you could just understand that 10 comes one number after 9.

In other words, you memorized a table.

[Spencer]

Just knowing that a number comes one number after another is knowing that X+1=y and that Y-1=x.

What's the rule for remember this?

[phandaal]

You need a table to remember that? Sweet baby jeesus.

[Spencer]

You need a table to remember that 9+6=10+5? Sweet baby jeebus.

[phandaal]

...did you just burn yourself? This is definitely more entertaining than doing work.

[Spencer]

No, I showed that you needn't have a table to remember it. You just learn it and remember it. You don't need a rule telling you why it is. it just is.

[MegaloMonocle]

Yeah. When you were a wee tad, you memorized basic addition and subtraction tables.

By now, they are so deeply wired into your brain you think you "just know". But you learned that 9 + 1 = 10 by memorizing a table.

[phandaal]

Yes, thank you for helping me remember my childhood.

[Red Rocks Rockin]

Or you could just understand that 10 comes one number after 9. And you're not subtracting anything from the 6, you're just breaking it down into parts and adding those parts how you want.

Or you could just understand that 9+6 = 15, without taking 10 extra steps to get there.

[Robert]

It might help if done in conjunction with an abacus. Not the type of abacus they used to use with New Math, but the Chinese type where you can slide something to add or subtract 5.

[Spencer]

actually 9+6 = 15 because you've added 6 more to the nine, making it 15. MORON. What you just typed is like saying it's actually because 9+1=1-+1=11+1=12+1=13+1=14+1=15.

Actually, why not break down the 9 too. It's not a hard concept to understand. It's a STUPID concept to teach. They mean the same thing- and kids can think about it that way if they want or need to, but to teach a whole class just so morons who can only deal in multiples of 5 can get it is horrible.

[phandaal]

It's not multiples of 5. The number just happens to be 15.

That's how I taught myself when the teachers were making us memorize things. Why waste time learning a table when you can learn a rule that will make a table for you?

[Spencer]

Because the using the rule every time is stupid when you could just know the information. Hell, why learn anything when you can just look it up?

Yes, it's not multiples of 5- it's to add whatever in 10s because someone thought that was intrinsically better than 2s or 5s. You can do it however works for you- but if you force the class to think of a rule every time about the most simplest of things (especially if that rule complicates things twice over to get there) you've wasted everyone's time and made everyone know less.

[Griffin3]

I don't think phandaal has ever tried teaching this stuff to the sort of young children that might be learning single digit addition. I personally wonder if any of these very smart people who come up with these common core "alternate methods" have dealt with the children they are writing the methods for.

When you are teaching children the concept of addition, you can count beans, and regroup, and do all sorts of wacky things. Once they have the concept, you move on to the algorithms of math. Carrying, regrouping, long multiplication. If the child has to derive a table, or work out a rule, every time they need an addition or multiplication fact, they are hindered in every operation from basic math onward.

Kids need to learn the tables, and drill them until they come fast. It takes a month and a half, and sets a foundation that makes the next two years of math algorithms come easily. Try that on for comfortable.

[phandaal]

I used to tutor kids of many different ages in math, actually.

But you don't know me from Adam, I could be making this up. I promise I'm not a cop.

[phandaal]

I should add, I only ever got the problem kids, who are often smarter than the other kids. So there's that.

[Azathoth!!]

I used to tutor kids of many different ages in math, actually

But you don't know what subtraction is.

And you're not subtracting anything from the 6, you're just breaking it down into parts

I pity those kids if they're real.

[jace]

Rote memorization has its place. I only remember the multiplication table from elementary school, did they have an addition table, too? I would, heh, count addition as fancy counting, the first math any child learns, 1,2,3... by Little League you get fancy, counting by twos - "2,4,6, 8 who do we appreciate..." - Would you teach your 3 year-old some new way to learn counting other than nightly readings, daily games repetitively listing the order of the ordinals?
Note there is no need for a subtraction table, nor division, because they are inverse operations, having mastered (by rote memorization) addition/multiplication their inverse operations are much easier to learn. How is long division being taught in common core?

[avocats]

Look at the video for 3x3. She draws an array of 3x3 x's then goes through analysis AND COUNTING to get the result that 3x3=9.

[Agammamon]

9 + 6 = 15 BECAUSE part of the number 6 goes to make the 9 a 10, leaving you with 5.

[Agammamon]

Fuck you squirrels

[ant1sthenes]

It isn't a question of whether a child memorizes number tables, of course they're going to memorize number tables. 2+3 = 5 isn't something you reason out each time you sit down to add a couple of numbers, you just know it.

It's just a question of whether they memorize all the additions that take single digit numbers as inputs, or only the additions that result in a single digit number or 10 as an output. Of course, to do the latter, they have to have some quick way of knowing whether the result of the operation is greater than 10, so they're at least partially memorizing all of the single-digit additions anyway.

Now, the decomp way of thinking about things is fine in terms of teaching kids the skill of visualizing and arranging numbers, and how to be comfortable with breaking them down and putting them together. It just isn't usually as efficient as memorization for actually fucking solving problems (though a calculator is even better).

In programming terms, it's one thing to teach kids how to write up their own version of a queue class, and another thing to teach them to actually do that in an actual application rather than just using, say, an STL queue.

[John]

And the science says memorization is the best way for kids to learn basic arithmetic. But don't let the science get in the way of a good cargo cult.

http://www.startribune.com/science/272214111.html

[Pope Jimbo]

I can't believe that I will agree with something printed in the Red Star and Tribune, but I sure agee with that.

My kids' elementary schools all did some sort of crazy version of this crap. I think they called it whole math or something like that. Lots of homework where you were supposed to draw 9 apple and then 6 more apples next to it. Finally you counted all your apples and write the answer down.

I had a lot of conflicts about this with the teachers because I told them that - while it sucked - pages and pages of addition and subtraction problems are the best way to learn math. I then made my kids do tons of flash cards with me.

All three of them tested off the charts for their grade levels because they simply knew the basic addition/subtraction/multiplication/division tables by heart.

[HazelMeade]

I actually kind of "get" the new math in common core.

What they are really doing is using math as a vehicle to teach abstract reasoning. Which is actually kind of awesome.

I do fear that they might be teaching over the students heads though,and will end up leaving those who can't master the abstract reasoning with worse math skills.

[robc]

Abstract reasoning needs to wait until later. I think puberty, actually.

Is there reasons to think that the brain doesnt develop new abilities at that time too?

[Spencer]

NO, they are using abstract reasoning to teach math- sort of. It's dumb. there are only so many ways to add 0-9 together. Just memorize them and you can always have that knowledge. It's not that hard.

[HazelMeade]

I don't see why they can't do both.

Have like a "Basic math Skills" class, where they do rote memorization of tables. And then have an "Abstract Math" class where they play around with numbers and come up with clever ways to add and subtract more efficiently in your head.

[robc]

It already exists, its called "algebra"

[HazelMeade]

Thing is, remember when we were kids and everyone who was good at math used to say that the way math was taught was stupid because they made it boring? But if you LIKED math, you usually liked it because you knew how to play these games with numbers. That's what made math fun.
Well, rote memorization is boring.
This sort of thing? Subtracting 1 from 6 to add it to the 9 to get 10 and 5? That is the FUN Math, that was the way that we always wished our teachers would teacher when we were 8.

[Red Rocks Rockin]

But if you LIKED math, you usually liked it because you knew how to play these games with numbers.

As I pointed out above, the people who liked math were already making these intuitive leaps because they'd mastered the fundamentals ahead of their peers. Common Core doesn't do that--it presumes that abstract reasoning is all that is needed, without a solid grounding in knowledge of the basics.

You know why Vince Lombardi was a great coach? Because every year, he'd start training camp by telling everyone from the rookies to the 10-year veterans, "Gentlemen, this is a football." He'd ground them in fundamentals at the start of every year and build from there, sometimes running the same play over and over in practice for 20 minutes until the players could do it in their sleep. He understood that needlessly complicating effort created friction and degraded performance.

[Spencer]

Yes. That's fine. But they needn't make all students waste time by forcing them to learn basic arithmetic via abstract reasoning.

Children at a certain age aren't able to understand abstract reasoning.

[phandaal]

Careful. The dream team is about to drop some "knowledge" on you.

[Spencer]

And phandaal is about to make assertions without facts in evidence to support his mindless support.

[phandaal]

I've already done that, as well as built and burned some lovely strawmen. No need to repeat myself.

[Acosmist]

Kids already can't understand math at grade level. This ain't helping.

[Solomon Grundy]

They're not teaching abstract reasoning, they're teaching a torturous procedure for doing something you're going to have to do fast in higher grades. 90% of the kids are just going to memorize what the procedure is and not related it to anything outside the problems on the homework and test.

[DEATFBIRSECIA]

Un. Fucking. Believable.

[NYC Liberal]

I really don't see the point of doing math this way.

I am for a common core curriculum. But I need to ask God: Why? Why this curriculum in this manner? Can't we just have a national standard that says Grade X students must know a,b,c by June 1st?

[robc]

You are opposed to unschooling then I guess.

Well fuck off then.

[MegaloMonocle]

I am for a common core curriculum dictated by the federal government.

What could possibly go wrong?

[ant1sthenes]

Well, for one thing, it assumes that students are all the same -- either you're pushing students too hard (and punishing teachers unfairly) in areas where they are weak, or you aren't pushing teachers to help gifted students make the most of their unique talents.

Anyone who has multiple kids probably sees some variance in development for even basic things like mobility, speech, potty training, etc. In the long run, it tends to even out, but if you had some monthly chart of where your kid was supposed to be, it would be a nightmare (I say monthly instead of yearly, because physical and mental development is happening much faster than at later ages).

Ideally, the education establishment would drop the idiotic five year plans and age-based segregation and just figure out how to focus on moving each student along the path of knowledge at the appropriate pace. I think it's doable, especially as schools use more software to aid teachers.

[robc]

I thought this would be a mostly dead thread in which I posted once or twice.

Because, holy fuck, people actually support this shit.

[Spencer]

People who think this way think everyone should think this way. They don't realize that they are making things harder and more inefficient and most people would be slowed down to think this way.

But if you tell someone they think slower they think you're calling them stupid and rush to defend their way as the one true correct, best way.

[heartburn]

10 is your friend... in the same way that big government is your friend.

[Spencer]

I want to put "10 is your friend..." on a t-shirt.

Reason needs a tshirt shop online where the content is taken solely from the comment sections.

[heartburn]

They should put autoplay sucks on a t-shirt.

[robc]

Cafe Press does t-shirts on demand.

We need a "publish this to cafe press" button on each comment.

[Spencer]

Yes. Make it so.

[MegaloMonocle]

Two subtractions (10 - 9 and 6 - 1).

And then two additions (9 + 1 and 10 + 5).

We've now turned a single mathematical operation into four separate mathematical operations.

Why does it not surprise me that a bunch of government bureaucrats require an unnecessarily long and complicated process to get to a pretty obvious result?

[Dweebston]

If their procedure produced an obviously erroneous result which they swore by anyway, it would be even less surprising.

[Zeb]

Breaking things down into parts that are relatively easy to deal with is how people generally solve difficult problems. Learning the technique on simple problems doesn't seem like a terrible thing to introduce students to. When learning about math, you usually start with simple and obvious examples.

Of course, I am sure a lot of teachers won'y be thinking about it this way and this will just become annoying thing for kids to do and then forget. But I honestly think that the idea is a pretty good one.

[CatoTheElder]

That the 9+6 "decomposition" is a "math fact" is a basic misunderstanding of math. The "decomposition" is a specific application of the associative law of addition to the numbers 9 and 6. Here's a math fact: 9+16=15. Whether kids should memorize math facts before they learn abstract laws of binary operations should be thoroughly researched before this program is implemented. I suspect that Feynmann's observation about field testing in educational theory and practice applies here just like it did when he was involved in California physics education.

The addition algorithm is far less efficient than the old-school method. In the real world, people have to add numbers like 37.23+44.35+157.77. If you can't look at those numbers, and quickly estimate a sum of 238 in your head (or even quicker, 240 if only two digit accuracy is suitable), and add them up in a column for a precise answer in a bit more time, you're innumerate. The algorithm presented is not up to task for any type of practical addition.

Ultimately the kid has to memorize 9+6=15 one way or another. The kid also needs to understand that 9+6=9+(1+5)=(9+1)+5. The decomposition method might be a good trick to facilitate memorization. I don't know because I don't know whether "young learners" are better able to learn about commutative and associative properties before they learn the elementary basics of arithmetic.

[Zeb]

I disagree. I don't really have memorized that 9+6 is 15. I just figure it out really fast. And the algorithm they lay out is pretty much exactly how I do mental arithmetic. Which I am pretty good at.

And the "math fact" that they refer to is that 9+6=15.

[jdd6y]

It seems crazy to introduce concepts such as a base system to 1st graders who are trying to learn simple, pre-K level math (i.e., already not that bright). How many people with advanced degrees even know that there are bases other than 10?

Isn't this stuff suppose to "solve" the fact that the bottom 50% of kids can't do math well? I.e., focused on the doofuses?

Kids with aptitude understand the concept of oneness, twoness, etc, and a simple operation such as addition easily.

But now we are going to insert the concept of base systems to those who don't get this stuff easily? Hey, Jimmy, well, 9+16=15 in base 10, but what's the answer in base 12? Why can't you do this problem in a Z3 system?

The human brain develops over time and I'd bet than no more than 10% of 7 year olds learn best with concepts versus counting their own fingers and toes. Most kids of that age can't even sit still.

[RussianPrimeMinister]

I guess it turns out my grade school teachers were so incredibly stupid that they just couldn't understand the right way of teaching me to add. Now, for me, 2 + 3 = 9.

Thank you, federal government, for saving our children from the curse that is traditional teaching.

[Notorious G.K.C.]

The important part is that it makes parents feel stupid.

"You may be a big shot with a big job and a big paycheck and a big house, but *I* teach your kids, and you can't even help them with their homework!"

[Rich]

"Can you believe that dumb fuck never even heard of 'anchoring?!"

[Red Rocks Rockin]

The important part is that it makes parents feel stupid.

Actually, this wouldn't be too far from the truth.

Look at sabermetrics. The reason they're becoming so big in sports analysis now is because a bunch of stat nerds and then journalists wanted a way to differentiate their knowledge of the game from the average joe that watches the games. Take a look at a typical baseball article these days and its an alphabet soup of acronyms that the average person doesn't give a shit about, but are supposedly Very Important for measuring player performance.

Self-styled elites tend to needlessly complicate simple things in order to make themselves seem more knowledgeable than their peers. It's really nothing more than status-grasping.

[The Late P Brooks]

Is 10+5 intrinsically easier than 9+6?

If you wear flip-flops to school, yes.

[Spencer]

I was confused by this for longer than I would care to admit. I like it. Thank you.

[Kaptious Kristen]

If a kid more easily learns by going through all that shit to get 9+6, that's fine. If a kid learns better by rote, that's fine. What we should be striving for is an efficient and cost-effective way to make education more individualized rather than more uniform. It's a total waste of time and money trying to figure out a way everyone can learn the same way. Nobody learns the same way.

[phandaal]

This is probably the most important comment here. Trying to shoehorn every kid into a single method is a terrible idea.

[Notorious G.K.C.]

It's so simply, so very simple
That only a child can do it.

https://www.youtube.com/watch?v=UIKGV2cTgqA

[Derpetologist]

I'm waiting to see how the plan on teaching multiplication without rote learning.

Maybe next they can teach people to read without having the alphabet memorized.

[Solomon Grundy]

Distributive law.

5 x 7 = 5 x (10 - 3) = 50 - 15 = (50 - 10) - 5 = 40 - 5 = 35

I'm sure they'll have a great time solving equations in algebra using that method.

[userve32]

SOunds like some pretty serious business dude.

http://www.Crypt-Anon.tk

[userve32]

SOunds like some pretty serious business dude.

http://www.Crypt-Anon.tk

[userve32]

SOunds like some pretty serious business dude.

http://www.Crypt-Anon.tk

[Scarecrow Repair]

The original New Math anthem.

[Notorious G.K.C.]

Uh, EXCUSE ME?

http://reason.com/blog/2014/09.....nt_4747199

[Scarecrow Repair]

What, you got a monopoly or something?

[Scarecrow Repair]

And, pffft, Two against one, majority rules, bite me 🙂

[Notorious G.K.C.]

No thanks, I'm on a diet.

[Kabaragoyim]

No, Winston. Two plus two does not always equal four. Sometimes they are five, sometimes three.

- O'Brien

[Big Chief]

That's for Middle School. I love Big Brother!

[Warty]

This is approximately the way I do mental arithmetic. Common Core may be dumb, but this isn't a completely worthless way to think about math. It is probably a shitty way to teach it, but at least some kids will do it this way regardless.

[Zeb]

It does seem silly when they present the example with small numbers, but this is how a lot of people do math in their heads. Maybe more people will be better at mental arithmetic.

I don't have a problem with memorizing small sums and products, but I was always terrible at the timed tests and couldn't be bothered to memorize it. And I am a math major.

Depending on how it is presented in class, it could be really pointless, but I think that the idea is pretty sound. The biggest problem I can see is that everyone will probably have to do it this way rather than be allowed to use whatever works best for each student.

As I see it, the problem here is far more with public schools and people who want to standardize education than any of hte actual content of common core standards (at least for math).

[Solomon Grundy]

And I am a math major.

Math at the college level has very little to do with arithmetic, so that doesn't provide much cred.

But you must have had fun solving

4x - 8y - 6 = 6
8x + 4y + 5 = -9

in algebra (and every math class that follows) if this is your method of addition.

Long story short, regardless of how neat and theoretically nice these methods seem, these kids are going to have to unlearn what they've been taught to actually do real math problems in a few years. You do NOT want to teach something you're later going to have to unteach. That's like the first rule of teaching.

[Zeb]

Well, it is what I do, as do several other commenters on this thread, only I do it very quickly. Maybe not for small numbers. I probably have that mostly just memorized.

If this is what they are presenting as the only way to do addition, that's stupid. But it is a good way to think about it for some people.

[Fluffy]

Personally when I am asked simple addition of three digit numbers or less I simply see the answer in my head and can give it.

The answer is the important thing. Every teacher I ever had who defied this simple principle was a worthless cunt who deserved a violent death. Now they've institutionalized that cuntiness.

[Solomon Grundy]

How results-oriented for libertarians who place so much emphasis on principles.

[jace]

If this is how it will be commonly taught, students will need to 'show their work'-- while it might be helpful for some to do it mentally 'in their head' - showing it will frustrate many students. And the students that can make friends with 10 and decompose 6 will get straight As (even if they decompose 6 as 1 and 4, because they got the concept!)

[Christophe]

9 + 6 = (9+1) + (6-1) = 10 + 5 = 15

Ok, but why 1? 9 + 6 = (9+X) + (6-X) for any X, whether that's 1, 30, -8, or sqrt(-?).

I get that they want to teach the why of addition, but they've left the most important step out of their process. So the kid sees this and then you give it 5 + 7, and he's totally fucked (assuming he hasn't already gotten addition down, and is just reverse engineering your technique from the answer, which happens all too often).

I love having a "slow but trivially easy" method when mentoring someone in math. But it isn't trivial if they have to pull a magic constant from their butts in order to make progress.

If you want to give a kid a fallback for addition, the only thing to do is repeated increment/decrement. 9+6 = 10+5 = 11+4 = 12+3 = 13+2 = 14+1 = 15+0. It's brain dead easy, there's no magic constants involved, and it's horribly slow, so they'll quickly move on to memorizing the tables, once they're comfortable.

[Solomon Grundy]

It's even simpler than that. If they know how to count high enough, all they need to do is count out the next 6 numbers after 9, and the answer is the last number they count. (if they don't know how to count they're going to have trouble regardless of what method you teach)

In fact, this is roughly how addition is defined in most abstract algebra constructions of the integers.

[BiMonSciFiCon]

Are kids graded on their ability to answer questions in this "special" way? Or can they just write "15"?

[Francisco d'Anconia]

Robby, what the fuck? Repost this without the autoplay. Every time I reload H&R for the next 24 hours, that fucker is gonna play.

[Steve G]

Why am I picturing Robby in the office leaning over his shoulder, "Hey guys, watch this shit. Imma about to make the commentariat blow a gasket"

[pronomian]

Wow. Instead of anchoring the 9 to a 10, then add the 10 to the 5, make the 9 into a 10 then add the 6, you get 16, then find out how much is the 10 from the 9, 1, then subtract that from the first final answer, 16 and you get 15.

[Zeb]

Yeah. A better way to teach this would be to show that there are many ways you can manipulate numbers and let them figure out what works better for them.

[pronomian]

I don't understand, without going back as far as those who came up with uses for gun powder, developing weaponry, building infrastructures, we had people figure out how to make a computer, correct me if I'm wrong, I think there was math involved in that, we had people using math to figure out how to get a man to the moon and back. At what time did they have the need to link the first number to a ten, did they learn using common core then? Instead of dumbing crap down to the lowest denominator (sorry, that's math talk) why not try to elevate to the highest?

[Bramblyspam]

This common core method is exactly how I do math in my head. 9+6 equals 10+5 equals 15.

The problem, such as it is, is that the explanation is way confusing to anyone who doesn't already know the method they're trying to explain.

[Solomon Grundy]

Please don't tell me you use the distributive law to figure 5 x 7.

I love the field axioms as much as anyone but they have no place in first grade math.

[Zeb]

Sure they do. You don't introduce the idea of axioms, but you can get kids to make intuitive sense of the laws early on. How do you do multiplication of larger numbers if you don't introduce the distributive property?

[Solomon Grundy]

You don't introduce it in its full level of abstraction, which is what you'd have to do to figure out 5x7 without memorization.

The way people figure out multiplication on paper does use the distributive property of course, but it's hidden in the very simple method (ie adding multiples of declining powers of 10). You don't want to condemn a kid who has a hard time with abstraction to never being able to multiply numbers.

[Zeb]

I don't know. I would teach that 5*7=7+7+7+7+7 before I had kids memorize multiplication tables.

[Solomon Grundy]

How do you suggest they compute 7+7+7+7+7 ?

[jace]

Recusively! I don't know what 7+7 is but I know how to count!- I'll keep decreasing 7 until it's 1. Then move the first 7 one over on the number line. Gosh I have to do that 4 more times. Don't forget to show your work. (I'm thinking kids are gonna hate math, reminds me of tree diagrams: If Suzie can choose to wear her blue shirt, or red shirt with her skorts or pants and her white, blue, or red shoes how many outfits can Suzie make? Draw a tree diagram to illustrate the solution)

[Solomon Grundy]

How many minutes are you going to spend figuring out 5x7 ?

[Zeb]

Who says that's what you have to do every time? I'm just saying they should know what it is that they are learning to do. And that involves introducing concepts like distributivity. And that if you learn that, you will likely be better at doing mental arithmetic. This started with you saying that field axioms don't have a place in first grade math. They most certainly do. That doesn't mean that they replace becoming familiar with basic sums.

[Solomon Grundy]

I'm just saying they should know what it is that they are learning to do.

Cool, demonstrate that ONCE with products involving numbers less than 4. One day of their lives. Then you move on to the practical method they're going to use every time.

You absolutely do not want to teach them to see 5x7 as 7+7+7+7+7 ever again. At least not until they have an extremely unusual problem where that view is advantageous -- a highly unlikely situation.

[Zeb]

Why the fuck would anyone keep seeing it that way if there was an easier way to do it? What is your problem? Who are you arguing with? No one ever said that kids should't learn to do simple arithmetic quickly, which most will do most effectively by memorizing it. All I have said is that you teach the concept behind it first.

[Solomon Grundy]

We were talking about how to compute 5x7 when you brought up that 5x7=7+7+7+7+7. Forgive me for connecting the two subjects.

[Zeb]

Exactly. Adding is counting, multiplication is iterated addition. And I am pretty sure most first graders are capable of understanding what addition is. I think kids should know that before memorizing sums and products. I have no problem with memorizing your multiplication tables, but you should know what it is that you are memorizing.

[Solomon Grundy]

Are they supposed to learn 6834 x 9247 the same way? Where do you stop?

[Zeb]

No, of course not. You are not seriously this fucking dense. You do that in the conventional way, or use a calculator. But you learn what it is that you are doing when multiplying two numbers before you memorize your multiplication table.

This whole argument is in response to you saying "I love the field axioms as much as anyone but they have no place in first grade math." I never said that learning more efficient ways to do it was a bad idea.

[Solomon Grundy]

I guess I missed the fact that there was another incredibly clumsy, inefficient way to do 5x7 besides using the distributive property. My bad.

My point is that (a) abstract properties such as the distributive law are going to confuse and frustrate many students who may otherwise have been able to be good at arithmetic; and (b) the efficient way should be introduced ASAP after introducing the basic definition. The basic definition should not be dwelt on in early grades.

[Bruce D]

6834 x 9247 = 6834 x (9250 - 3)
= 6834 (9250) - 3(6834)
= 6800(9250) + 30(9250) + 4(9250) -3(6800) - 3(30) - 3(4)
= 6800(9250) + (270,000 + 7,500) + (36,000 + 1,000) -3(6800) -90 - 12
= 6000(9250) + 800(9250) + 277,500 + 37,000 -3(6000) -3(800) - 90 - 12
= 200(277,500) + 200(37,000) + 277,500 + 37,000 -3(6000) -3(800) - 90 - 12
= 55,500,000 + 7,400,000 + 277,500 + 37,000 -18,000 -2,400 - 90 - 12
= 55,500,000 + 5,000,000 + 2,400,000 + 270,000 + 7,500 + 37,000 - 20,400 - 90 - 12
= 60,500,000 + 2,400,000 + 270,000 + 7,500 + 37,000 - 20,400 - 90 - 12
= 62,900,000 + 270,000 + 7,500 + 37,000 -20,400 - 90 - 12
= 62,900,000 + 100,000 + 170,000 + 7,500 + 37,000 - 20,000 - 400 - 90 - 12
= 63,000,000 + 177,500 + 10,000 + 7,000 - 400 - 102
= 63,000,000 + 187,500 + 7,000 - 500 -2
= 63,000,000 + 194,500 - 500 -2
= 63,000,000 + 194,000 - 2
= 63,194,000 - 2
= 63,193,998

[HazelMeade]

Yes, after a certain point, just memorize the tables.

The thing is, to me it makes sense to teach things like 7+7+7+7+7 FIRST, and then do multiplication tables once they get bored of that.

[Hayeksplosives]

I agree. One of the big problems with Common Core math is that it specifies the exact method of finding the solution, demanding the student show their work in the expected way, and not everyone uses the same method.

[Zeb]

I had a great math teacher who said "if it works, do it". If you could find a method to solve a problem and demonstrate that your method was valid, that was OK however you did it.

[Solomon Grundy]

I had super-Aspie kids in calculus who, when I introduced the sum, difference, and power rules, pledged to ignore them and always do derivatives using the fundamental limit definition because they liked the idea. I told them that they were going to be in a boatload of trouble once we got to harder problems, and forbade them from using the definition of the derivative where one of the rules introduced in class already applies, under pain of having points taken off on homeworks and/or tests.

But you're right, I should have just told them if it works, do it. Then they'd be swimming in limits when we started taking derivatives of quotients, and be weeks behind their classmates when they finally gave up and admitted it didn't work so well after all.

[HazelMeade]

Or, they could end up being super math-geniuses who could do complex limit equations in their heads.
They could then use that math to solve so mind blowing quantum physics problem.

[Solomon Grundy]

No, they wouldn't.

[Zeb]

Oh, for fuck's sake. Are you just an asshole all the time? Or one of those super Aspie kids yourself?

You really think that's all he ever had to say on the subject? Or that he wouldn't say anything if your technique was horribly inefficient? He'd give you credit for solving the problem. Which is good in an 8th grade math class meant to encourage kids who had shown ability for math.

[Solomon Grundy]

You really think that's all he ever had to say on the subject? Or that he wouldn't say anything if your technique was horribly inefficient?

From what you described I did.

If you could find a method to solve a problem and demonstrate that your method was valid, that was OK however you did it.

[Zeb]

Well, you have very little imagination, it would seem. Or a very low opinion of people you don't know.

[Solomon Grundy]

My imagination is supposed to fill in details that your statements expressly deny?

No, I don't like your teacher's attitude, to be frank. The tried and true, efficient method should be learned and practiced and seared into students' minds before any artistry is encouraged, period. Nobody's coming up with new and better ways to solve 8th grade math problems that have been known for 400+ years.

[HazelMeade]

I agree with this. As we discussed above, you could do the problem in several ways, such as by thinking of 6 and as 2 groups of 3 and 9 and 3 groups of 3 and thus making 5 groups of 3, hence 15.

But if common core specifies the HOW, then it is defeating the purpose of teaching abstract reasoning. There are always multiple ways of reasoning to the same answer, and forcing people to learn only one way of reasoning is stifling.

[GILMORE]

Autoplay Video is a Hate Crime

[Hayeksplosives]

Could it be designed to erase the advantage that boys have (on average) over girls in scoring on math proficiency tests? By forcing them to learn a specific (and somewhat arbitrary) process for arriving at results, they eliminate the one subject where even undisciplined young boys can shine without absorbing and imitating everything that the teacher has to say.

[Solomon Grundy]

Sounds like a mansplanation to me.

[Solomon Grundy]

Of course the whole thing would be easier if they taught addition in binary.

[The Bearded Hobbit]

Without replying to a single thread I see that there are people who GET this concept and people who do not. I don't know exactly how to describe it but some people think of numbers as objects ("this 6 is carved out of a piece of stone") and people who see numbers as concepts ("what do I need to make this number a 10?"). I recognized the latter in about second grade, circa 1959. I think that this is a fundamental difference in people. Math always was easy for me and I couldn't understand why others had so much problem. Later, I understood.

The contortions that people were doing above ("two subtractions! TWO") is simply second nature to me.

My grandkids were having troubles and I showed them the difference. It took a bit but they latched onto it.

I did have to go thru the 1960's version of Common Core, "New Math". In third grade I couldn't figure out how division worked and neither could my dad. After an hour or so of frustration he simply showed me how to do division, thus ending my foray into "New Math".

And I kicked ass in story problems.

... Hobbit

[Fluffy]

This is ENTIRELY about seizing control of standardized testing to try to eliminate the advantage enjoyed by intelligent students and home schooled students.

An intelligent kid needs to go through flash cards of addition maybe TWICE and they'll know it. If you administer a test of addition problems to homeschooled intelligent kids taught the old way, they will all ace the test.

But public school teachers HATE THAT. So now they have a way to give standardized tests that don't do something straightforward Iike offer math problems for kids to answer. Now they can present bullshit absurd questions built around METHOD that have nothing to do with the actual ANSWER.

[Red Rocks Rockin]

But public school teachers HATE THAT. So now they have a way to give standardized tests that don't do something straightforward Iike offer math problems for kids to answer.

Actually, from what I've seen most teachers hate this method, because it creates more work for them when it comes time to grade homework and tests.

It's a lot quicker and easier to grade 50 questions of simple equations than it is to grade 50 questions of process mathematics.

[Marktaylor]

The problem is that it's completely unnecessary. Everyone understands the concept of basic addition even if it started with memorization because it's so simple. There are not adults, or even middle schoolers who can't grasp the concept of the basic functions (add, subtract, multiply, divide) so there is no reason to waste hours deconstructing the concept. If this was some higher math where people memorize formulas but can't grasp the concept like P values or some shit I could see breaking it down. Just tell them to memorize up to 12's and move on to harder math that needs more time.

[Response]

The reason we all had to learn the math tables was because we were given time limits (at least in my 3rd grade class). We knew the math. The math was easy. With the tables, they were wanting us to become proficient to the point of the thoughtlessness. I remember memorizing the entire random table pattern and trying to write down the numbers as fast as I could simply to compete with my class mates. I didn't do the math - I simply memorized the pattern. The thing is that we are trained to think in 10-based mathematics. Memorizing addition and multiplication tables is a natural basis for efficiency. Trying to add 1 to 9 to make 10 is more time consuming that simply knowing 1 + 9 = 10. The difference is subtle but also telling. It means that efficiency is no longer important. Which given the prevalence calculators everywhere is probably correct. The issue I have with the new math technique is how/why did they come up with 1 + 9 to get to the magic number 10 instead of 6 + 4. Why is 1 + 9 + 5 better than 9 + 6 or 6 + 4 + 5? Without an explanation, they just seem to be pulling crap out of their asses. At least with the tables you knew it was all about about efficiency.

[BohdanUke1]

Are you absolutely crazy? Haven't you heard that common sense is dead and buried?

We should thank our lucky charms that humanity made it this far without common core... But now we're saved!

[Will Nonya]

Why is she adding g and 6 in the first place?

[Mark22]

It's New Math!

https://www.youtube.com/watch?v=UIKGV2cTgqA

It's so simple, so very simple, that only a child could do it!

[Bruce D]

I've got a Master's in math and teach at junior colleges. That's one of the ways I do addition in my head. Though, when I teach remedial arithmetic, I expect the students to memorize addition and multiplication tables.

A better way of explaining the method is to how far from 10 is 9. Easy enough, it's 1. Then use definition of 6 to rewrite it as 1 + 5.

So 9 + 6 = 9 + (1 + 5) .....Definition of 6 as one more than 5
= (9 + 1) + 5 .....Associative Property of Addition
= 10 + 5 ..........Order of operations and definition of 1 as 1 + 9
= 15 ..............Definition of base 10 addition or definition of 15 as 10 + 5

[BohdanUke1]

Bruce, have a few drinks, sit back and then read aloud what you wrote... listen to yourself...

You'll find that you're emulating "Rube Goldberg". You've heard of Rube? Sure you have...

Teaching and learning should be fun. 'Nough said.

[brokencycle]

As you have all said, this is beyond retarded making an easy addition problem harder and more steps than it needs to be (more steps means more chances for mistakes).

Seriously, 9+6 isn't hard, and kids shouldn't need to be made "more comfortable with it." You know how kids get more comfortable with math? Making them do hundreds of practice problems.

What do I know though, for elementary school, I wasn't in a government school.

[Michael Hardy]

Yes, it does take longer to understand something than to just memorize and believe. But any adult who feels that these few trivial steps are a reason to pull one's hair out should be euthanized.

I memorized everything with everyone else. That gets you started, but that's all it does.

Robby Soave, you should be profoundly ashamed of yourself for appealing to the anxieties and cowardice of people who flunked out of elementary school and recruiting that sort of people as your allies and disciples.

[True Scottsman]

Are you really going to say that the commenters here who discussed, at length, the relative value of rote memorization vs critical thinking relative to the age of the student are mindless disciples of Some nefarious plot by Robby to... Well something. Good God man! Fuck off!

[Landon]

Whats funny is all my life this is EXACTLY how I do math. I can break data segments up in my head incredibly fast with this process, however I learned it on my own as a child and failed homework and tests in school for doing things this way. I was using the example with Sarah of how I figure out the difference between 1937 and 2014 in my head in seconds: My brain will add 3 to make it an even 1940 then subtract it from 2000 making 60 then I add the 3 back(63) then add the 14, which equals 77.

But would I force this method or any method on anyone-especially children?

No! I'm not an evil, brain cell killing bastard.

[Tamfang]

233 comments and no one mentioned Tom L.?

[True Scottsman]

Well, you did.

[BohdanUke1]

This is how they teach arithmetic on Planet Meshuga. I don't see a problem...

[ozzybroad]

my neighbor's step-aunt makes $74 /hour on the internet . She has been out of a job for seven months but last month her check was $12917 just working on the internet for a few hours.
find more information========== http://www.jobsfish.com

[goneGalt]

I'd like to see Common Core do the math on THAT post!

[vicbritpii]

my co-worker's step-sister makes $83 /hour on the laptop . She has been laid off for 8 months but last month her pay check was $15660 just working on the laptop for a few hours. see this here.....

============ http://www.netjob70.com

[HBfromMN]

We went out of our way to send our kids to a Common Core school, and these stories are just plain false. I suspect someone with a political agenda is planting these stories in a gullible media.

Common Core is based on the concept that there are certain things that everyone should know -- how to add, subtract, divide, and multiple, for example. Different schools may try different methods, but it has nothing to do with Common Core. Please don't buy into the political spin, because you may be inadvertently destroying one of the better curricula out there.

None of this is to say that Common Core should be a national standard -- it shouldn't. National standards for education are a mistake for many, many reasons, even a standard like Common Core, that I happen to think is excellent for my kids and my family. Know what you are fighting against, and don't throw out the baby with the bathwater.

[JPMcGrath]

Obviously, you are not mathematically inclined. I was a meth major, but long before that, in first grade I think, I figured this out and have used this approach ever since.

Let's take a more practical example. Say you have: 986 + 237 = ?. You could add the 7 and 6, which is 13, so you put down 3 and carry the 1. Next you have the 10's place, so you add 8 + 3, plus the 1 you carried, giving 12. You put down 2 and carry the 1. Finally, for the 100's place, you take 9 + 2 plus the 1 you carried, giving 12, so the answer is 1223.

Instead, you could just note that 986 is close to 1000, so you figure:

(986+14) + (237-14) = ?
(1000) + (223) = 1223

If you wonder how those geeks can add things up so quickly without a calculator, this is the kind of thing they use to do it. Those who are less analytical and more procedural minded might not make use of this, but many will.

Now, a journalism question: When you are writing about something and don't understand it, aren't you supposed to ask someone who does?

[iEagleHammer]

Spare us the I'm a math (not meth?) major BS. You don't want to get into that battle.

I have seen first hand how this confuses kids. procedural addition is simpler. Show the same kids the simple way to do addition, and they get it instantly. I could write out your more analytical method in a paragraph and make it seem complicated too. This method may be great, but you should show the kids the easiest way of solving the problem first.

Which leads us to the reporter in the video, she's a dunce. We learned to solve 9+6, not memorize it. If she tried to memorize it, that explains why she didn't choose a career in physics or engineering.

[ElDuderino]

I can't wait to for the day when these kids need to make change. My quarter-pounder is getting cold son, just keep the change.

[John Crofford]

By emphasizing "getting to anchor numbers" they are essentially making kids count back change as part of basic addition. I wouldn't worry about your change.

[ElDuderino]

Wow, there's a lot of debate here about the fundamentals of math and whether or not it's appropriate to teach young children this way.

The problem, as I see it is one of choice. Why are we so bent on forcing every school and every teacher to teach every subject the same exact way? If this doesn't work, then it fails everyone all at once.

Why don't we just hire teachers that we believe have the skills and knowledge to properly teach children these skills. Why don't we let each teacher decide how to teach math to first graders?

I suppose for my plan to allow each teacher to have the freedom to teach however they think best, we need to allow schools to fire those teachers who suck at doing that, but since the unions protect the shitty teachers and squeeze out the hiring of new and potentially better teachers, we need to have common core so the shitty teachers don't have to strain themselves with actually teaching children.

[Real American]

how the fuck do students know that 6 is "decompressed" (what a stupid fucking term!) into 1+5? Why isn't it decompressed into 2+4 or 3+3 or 4+2 or 5+1? There's no fucking 10 in any of those equations. If there's not a 10 how will the students fucking learn? And how the fuck do they know that 9+1=10 if they didn't already fucking memorize the answer?

why make simple shit complicated? oh, right. the left believes they can rewire humans to make them perfect.